資源簡(jiǎn)介

1、如圖，已知C是線段AB上的任意一點(diǎn)（端點(diǎn)除外），分別以AC、BC為斜邊并且在AB的同一側(cè)作等腰直角△ACD和△BCE，連接AE交CD于M，連接BD交CE于N．給出以下四個(gè)結(jié)論：①M(fèi)N∥AB；② ；③ ．④AB=2MN；其中正確的結(jié)論有
①②③
①②③
（填寫(xiě)序號(hào)即可）
考點(diǎn)：相似三角形的判定與性質(zhì) ( http: / / www.21cnjy.com / " \o "歡迎登陸21世紀(jì)教育網(wǎng) )；等腰直角三角形 ( http: / / www.21cnjy.com / " \o "歡迎登陸21世紀(jì)教育網(wǎng) )．
專(zhuān)題：綜合題 ( http: / / www.21cnjy.com / " \o "歡迎登陸21世紀(jì)教育網(wǎng) )．
分析：（1）用平行線分線段成比例定理；
（2）根據(jù)相似三角形的性質(zhì)，化簡(jiǎn)分式可得；
（3）要利用二次函數(shù)最值即可求解．
（4）根據(jù)已知條件不能確定M、N分別是AE，BD的中點(diǎn)，也就不能確定④的正確性．
解答：解：（1）∵CD∥BE，
∴△CND∽△ENB，
∴ ①
∵CE∥AD，
∴△AMD∽△EMC，
∴ ②
∵等腰直角△ACD和△BCE，
∴CD=AD，BE=CE，
∴ ，
∴MN∥AB；
（2）∵CD∥BE，
∴△CND∽△ENB，
∴ ，
設(shè) =k，
則CN=kNE，DN=kNB，
∵M(jìn)N∥AB，
∴ = = ，
= = ，
∴ + =1，
∴ = + ；
（3）∵ = + ，
∴MN= = ，
設(shè)AB=a（常數(shù)），AC=x，
則MN= x（a-x）=- （x- a）2+ a≤ a；
（4）依題意不能確定M、N分別是AE，BD的中點(diǎn)，也就不能確定④的正確性．
故答案為：①②③．
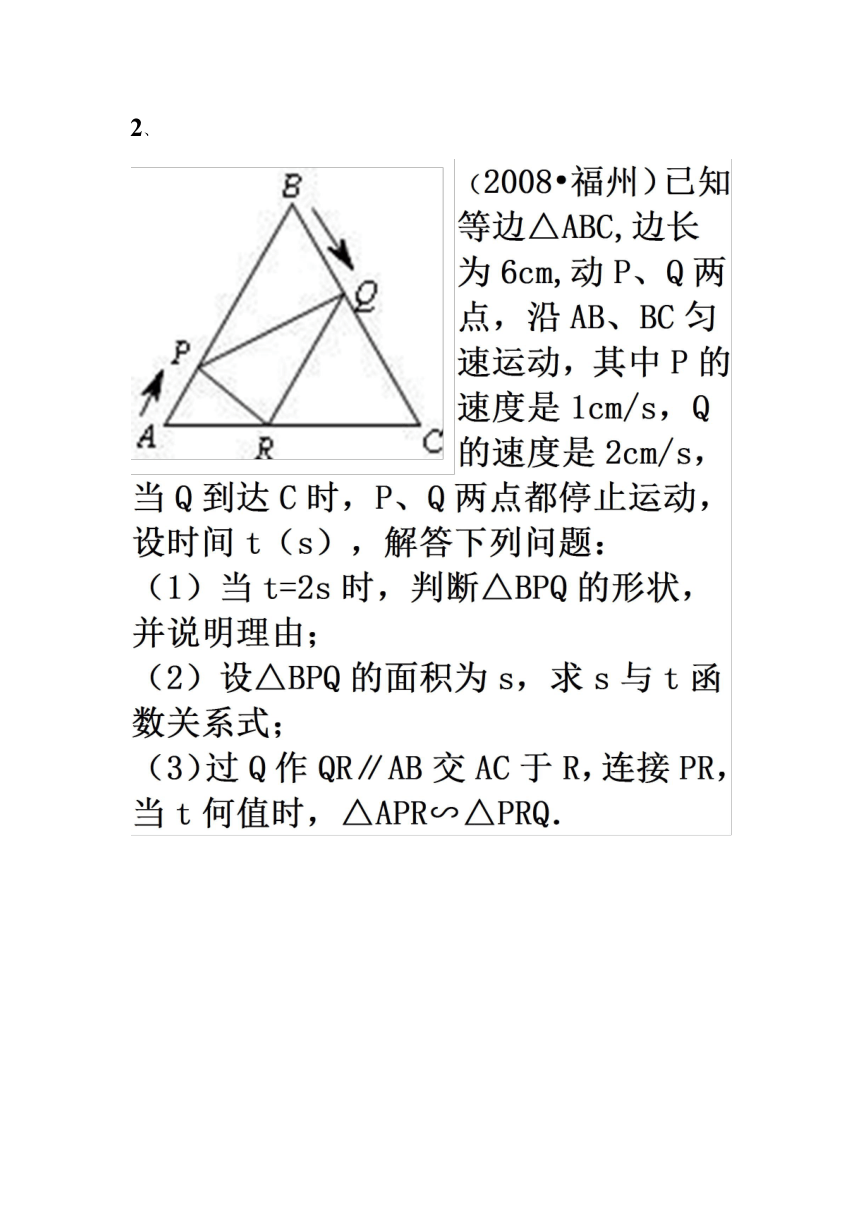
2.
2、
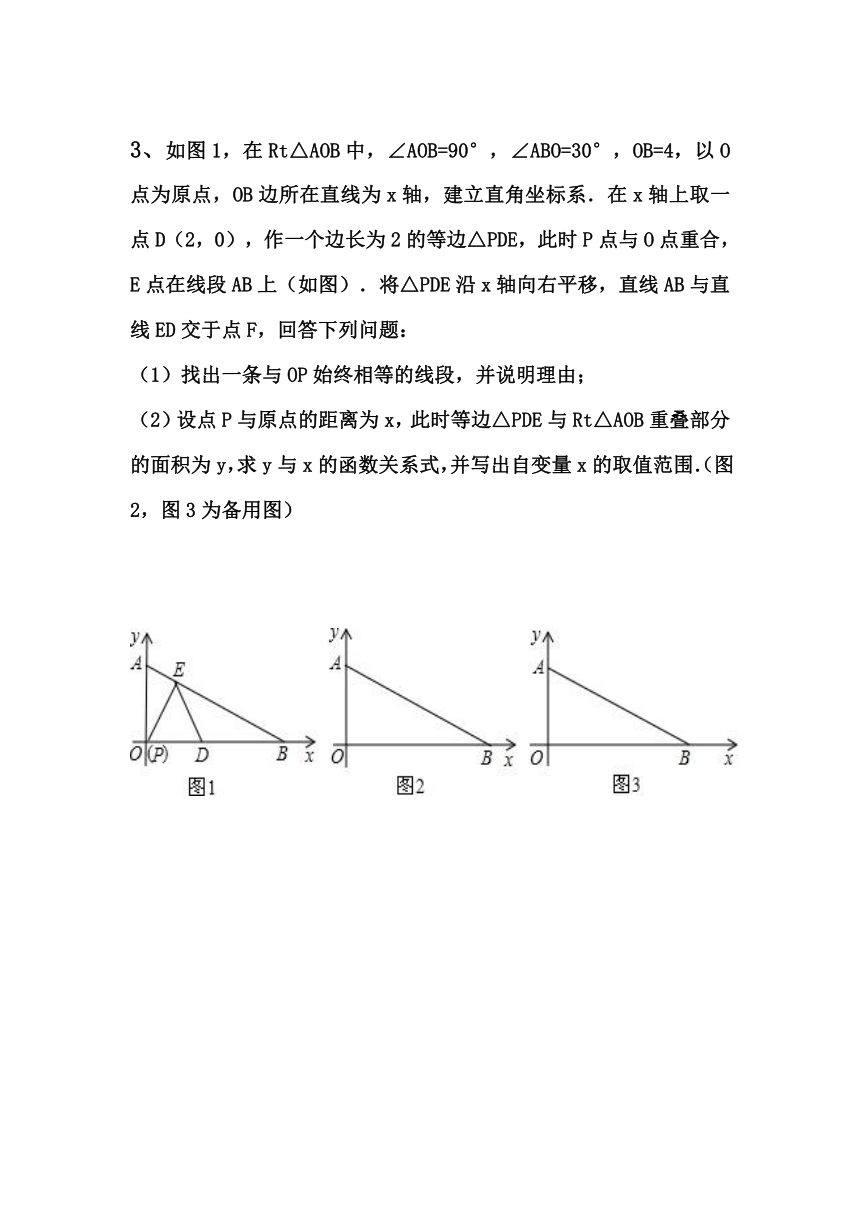
3、如圖1，在Rt△AOB中，∠AOB=90°，∠ABO=30°，OB=4，以O(shè)點(diǎn)為原點(diǎn)，OB邊所在直線為x軸，建立直角坐標(biāo)系．在x軸上取一點(diǎn)D（2，0），作一個(gè)邊長(zhǎng)為2的等邊△PDE，此時(shí)P點(diǎn)與O點(diǎn)重合，E點(diǎn)在線段AB上（如圖）．將△PDE沿x軸向右平移，直線AB與直線ED交于點(diǎn)F，回答下列問(wèn)題：
（1）找出一條與OP始終相等的線段，并說(shuō)明理由；
（2）設(shè)點(diǎn)P與原點(diǎn)的距離為x，此時(shí)等邊△PDE與Rt△AOB重疊部分的面積為y，求y與x的函數(shù)關(guān)系式，并寫(xiě)出自變量x的取值范圍．（圖2，圖3為備用圖）
4、（2006 蕪湖）在一次科學(xué)探究實(shí)驗(yàn)中，小明將半徑為5cm的圓形濾紙片按圖1所示的步驟進(jìn)行折疊，并圍成圓錐形．（1）取一漏斗，上部的圓錐形內(nèi)壁（忽略漏斗管口處）的母線OB長(zhǎng)為6cm，開(kāi)口圓的直徑為6cm．當(dāng)濾紙片重疊部分三層，且每層為圓時(shí)，濾紙圍成的圓錐形放入該漏斗中，能否緊貼此漏斗的內(nèi)壁（忽略漏斗管口處），請(qǐng)你用所學(xué)的數(shù)學(xué)知識(shí)說(shuō)明；
（2）假設(shè)有一特殊規(guī)格的漏斗，其母線長(zhǎng)為6cm，開(kāi)口圓的直徑為7.2cm，現(xiàn)將同樣大小的濾紙圍成重疊部分為三層的圓錐形，放入此漏斗中，且能緊貼漏斗內(nèi)壁．問(wèn)重疊部分每層的面積為多少？
解：解法一：
∵表面緊貼的兩圓錐形的側(cè)面展開(kāi)圖為圓心角相同的兩扇形，
∴表面是否緊貼只需考慮展開(kāi)圖的圓心角是否相等．
由于濾紙圍成的圓錐形只有最外層側(cè)面緊貼漏斗內(nèi)壁，故只考慮該濾紙圓錐最外層的側(cè)面和漏斗內(nèi)壁圓錐側(cè)面的關(guān)系．
將圓形濾紙片按圖示的步驟折成四層且每層為圓，
則圍成的圓錐形的側(cè)面積=（1-2×）S濾紙圓=S濾紙圓．
∴它的側(cè)面展開(kāi)圖是半圓，其圓心角為180度，
如將漏斗內(nèi)壁構(gòu)成的圓錐側(cè)面也抽象地展開(kāi)，展開(kāi)的扇形弧長(zhǎng)為：πd=π×6=6π（cm），
該側(cè)面展開(kāi)圖的圓心角為6π÷6×=180度．
由此可以看出兩圓錐的側(cè)面展開(kāi)得到的扇形，它們的圓心角相等．
∴該濾紙圍成的圓錐形必能緊貼漏斗內(nèi)壁．
解法二：
∵圓錐可以看作是等腰三角形圍繞其對(duì)稱軸旋轉(zhuǎn)而成的幾何圖形，其正視圖和側(cè)視圖皆為全等的等腰三角形，
∴如濾紙片能緊貼漏斗內(nèi)壁，由其兩母線和開(kāi)口圓的直徑構(gòu)成的等腰三角形必與漏斗兩母線和開(kāi)口圓的直徑構(gòu)成的等腰三角形相似或頂角相同．
根據(jù)題意可得，濾紙圍成的圓錐形開(kāi)口圓的圓周長(zhǎng)應(yīng)為（1-2×）×2π×5=5π（cm），
由此可得其開(kāi)口圓的直徑為5cm，
∵濾紙圓錐的兩母線長(zhǎng)和開(kāi)口圓的直徑都是5cm；漏斗兩母線長(zhǎng)和開(kāi)口圓的直徑都是6cm，
∴兩三角形皆為等邊三角形．
故兩等邊三角形相似且角相等，所以濾紙片能緊貼漏斗內(nèi)壁；
（2）如果抽象地將母線長(zhǎng)為6cm，開(kāi)口圓直徑為7.2cm的特殊規(guī)格的漏斗內(nèi)壁圓錐側(cè)面展開(kāi)，得到的扇形弧長(zhǎng)為7.2πcm，
圓心角為7.2π÷6×=216度，
濾紙片如緊貼漏斗壁，其圍成圓錐的最外層側(cè)面展開(kāi)圖的圓心角也應(yīng)為216°，
又∵重疊部分每層面積為圓形濾紙片的面積減去圍成圓錐的最外層側(cè)面展開(kāi)圖的面積的差的一半，
∴濾紙重疊部分每層面積=（25π-×25π）÷2=5π（cm2）．
5、如圖，將半徑為2，圓心角為60°的扇形紙片AOB，在直線l上向右作無(wú)滑動(dòng)的滾動(dòng)至扇形A′O′B′處，則頂點(diǎn)O經(jīng)過(guò)的路線總長(zhǎng)為
．
6、（2006 湛江）已知拋物線y=ax2+bx+2與x軸相交于點(diǎn)A（x1，0），B（x2，0）（x1＜x2），且x1，x2是方程x2-2x-3=0的兩個(gè)實(shí)數(shù)根，點(diǎn)C為拋物線與y軸的交點(diǎn)．
（1）求a，b的值；
（2）分別求出直線AC和BC的解析式；
（3）若動(dòng)直線y=m（0＜m＜2）與線段AC，BC分別相交于D，E兩點(diǎn)，則在x軸上是否存在點(diǎn)P，使得△DEP為等腰直角三角形？若存在，求出點(diǎn)P的坐標(biāo)；若不存在，說(shuō)明理由．
7、如圖，△ABC內(nèi)接于⊙O，其外角平分線AD交⊙O于DM⊥AC于M，下列結(jié)論：
①DB=DC；②AC-AB=2AM；③AC+AB=2CM；④s△ABD=2s△CBD
其中正確的有（　　）
8、以半圓中的一條弦BC（非直徑）為對(duì)稱軸將弧BC折疊后與直徑AB交于點(diǎn)D，若，且AB=10，則CB的長(zhǎng)為（）
A． B． C． D．4
10．如圖，填在各方格中的三個(gè)數(shù)之間均具有相同的規(guī)律，根據(jù)此規(guī)律，n的值是
A．48 B．56
C．63 D．74
11．如圖，等腰直角△ABC中，AC＝BC，∠ACB＝90°，AF為△ABC的角平分線，分別過(guò)點(diǎn)C、B作AF的垂線，垂足分別為E、D．以下結(jié)論：①CE＝DE＝BD；②AF＝2BD；③CE＋EF＝AE；④＝．其中結(jié)論正確的序號(hào)是
①②③ B．①②④
C．①③④ D．②③④
12．如圖，點(diǎn)P在雙曲線y＝（x＞0）上，以P為圓心的⊙P與兩坐標(biāo)軸都相切，點(diǎn)E為y軸負(fù)半軸上的一點(diǎn)，過(guò)點(diǎn)P作PF⊥PE交x軸于點(diǎn)F，若OF－OE＝6，則k的值是 ．
13、（本題滿分8分）如圖，四邊形ABCD內(nèi)接于⊙O，AB為⊙O的直徑，C為BD弧的中點(diǎn)，AC、BD交于點(diǎn)E．
（1）求證：△CBE∽△CAB；
（2）若S△CBE∶S△CAB ＝1∶4，求sin∠ABD的值．
14、（本題滿分10分）如圖（1），點(diǎn)M、N分別是正方形ABCD的邊AB、AD的中點(diǎn)，連接CN、DM．
（1）判斷CN、DM的數(shù)量關(guān)系與位置關(guān)系，并說(shuō)明理由；
（2）如圖（2），設(shè)CN、DM的交點(diǎn)為H，連接BH，求證：△BCH是等腰三角形；
（3）將△ADM沿DM翻折得到△A′DM，延長(zhǎng)MA′交DC的延長(zhǎng)線于點(diǎn)E，如圖（3），求tan∠DEM．
圖1 圖2 圖3
15、（本題滿分12分）如圖1，在平面直角坐標(biāo)系中，直線l：沿x軸翻折后，與x軸交于點(diǎn)A，與y軸交于點(diǎn)B，拋物線與y軸交于點(diǎn)D，與直線AB交于點(diǎn)E、點(diǎn)F（點(diǎn)F在點(diǎn)E的右側(cè)）．
（1）求直線AB的解析式；
（2）若線段DF∥x軸，求拋物線的解析式；
（3）如圖2，在（2）的條件下，過(guò)F作FH⊥x軸于點(diǎn)G，與直線l交于點(diǎn)H，在拋物線上是否存在P、Q兩點(diǎn)（點(diǎn)P在點(diǎn)Q的上方），PQ與AF交于點(diǎn)M，與FH交于點(diǎn)N，使得直線PQ既平分△AFH的周長(zhǎng)，又平分△AFH面積，如果存在，求出P、Q的坐標(biāo)，若不存在，請(qǐng)說(shuō)明理由．
第16題圖
O
y
x
20
50
10
20
（噸）
（元）
第15題圖

展開(kāi)更多......

收起↑