資源簡介

函數與導數-函數的圖象與性質
專題綜述
高考對于函數的考查是多方位的，但主線是函數性質的探求及應用.而圖象可以從總體上直觀地刻畫函數的性質，對函數的圖象與性質結合考查，以性質體現圖象，用圖象彰顯性質.經過一輪復習，對涉及函數圖象與性質的問題積累了基本的解題思路與方法，建立的思維的連貫性，二輪的重點是關注思維的深刻性.因此，解決函數問題時，利用數形結合思想，能后識圖、用圖，理解研究函數性質，解決方程根個數與不等式解集問題.
專題探究
探究1：圖象的識別問題
圖象識別問題比較靈活，對能力要求較高.基本思路是，從局部出發，排除錯誤選項，再從整體出發，結合函數性質，判斷函數整體變化趨勢.
（1）由解析式選圖象、由圖象選解析式
答題思路：排除法
仔細觀察4個選項中的圖象找區別，確定排除角度，排除的思路可以按照：
①定義域的角度、②奇偶性的角度、③特殊點的角度、④單調性的順序進行排除.
第一步:觀察圖象中的定義域是否有區別，或者求選項中函數的定義域與圖象是否一致；
第二步:判斷函數奇偶性；
第三步:利用特殊點
第四步:單調性，利用單調性性質判斷或求導.
（2）同一坐標系中兩個函數圖象的對比
前提：給出的兩個函數含有相同參數
答題思路：結合函數解析式及圖像分別求參數的取值范圍，參數取值范圍相同即可.
（3）實際問題識圖
答題思路：根據實際問題，列出函數解析式，分析函數模型，選擇圖象.
（2021.浙江卷）已知函數，，則為如圖的函數可能是（ ）
A. B.
C. D.
【審題視點】
給解析式選圖，或給圖選解析式的題目，都從圖象出發，研究定義域、奇偶性、特殊點、單調性，排除選項.
【思維引導】
給圖選解析式，觀察圖象特點，選擇切入點，如上圖圖象關于原點對稱，軸右側的圖象先增后減，且極大值點在的左側，有針對性的排除選項.
【規范解析】
切入點一：圖象關于原點對稱函數為奇函數
選項：；選項：；兩個函數
為非奇非偶函數，故排除；
切入點二：單調性軸右側圖象先增后減，極大值點小于
選項：
當時，，函數在區間上單調遞增，
故排除；
故選.
【探究總結】
識圖題在高考中出現頻率較高，但有規律可循，圖象本身帶有較多的信息，從定義域，奇偶性、特殊點、單調性的角度足以排除錯誤選項.觀察圖象時，特別注意圖象是否有不經過的點，或者漸近線，考慮定義域；坐標軸上是否有坐標，可以用這些坐標作參照研究函數值、極值等；單調性的問題上，可以用單調性性的性質初步判斷，再用導數判斷.
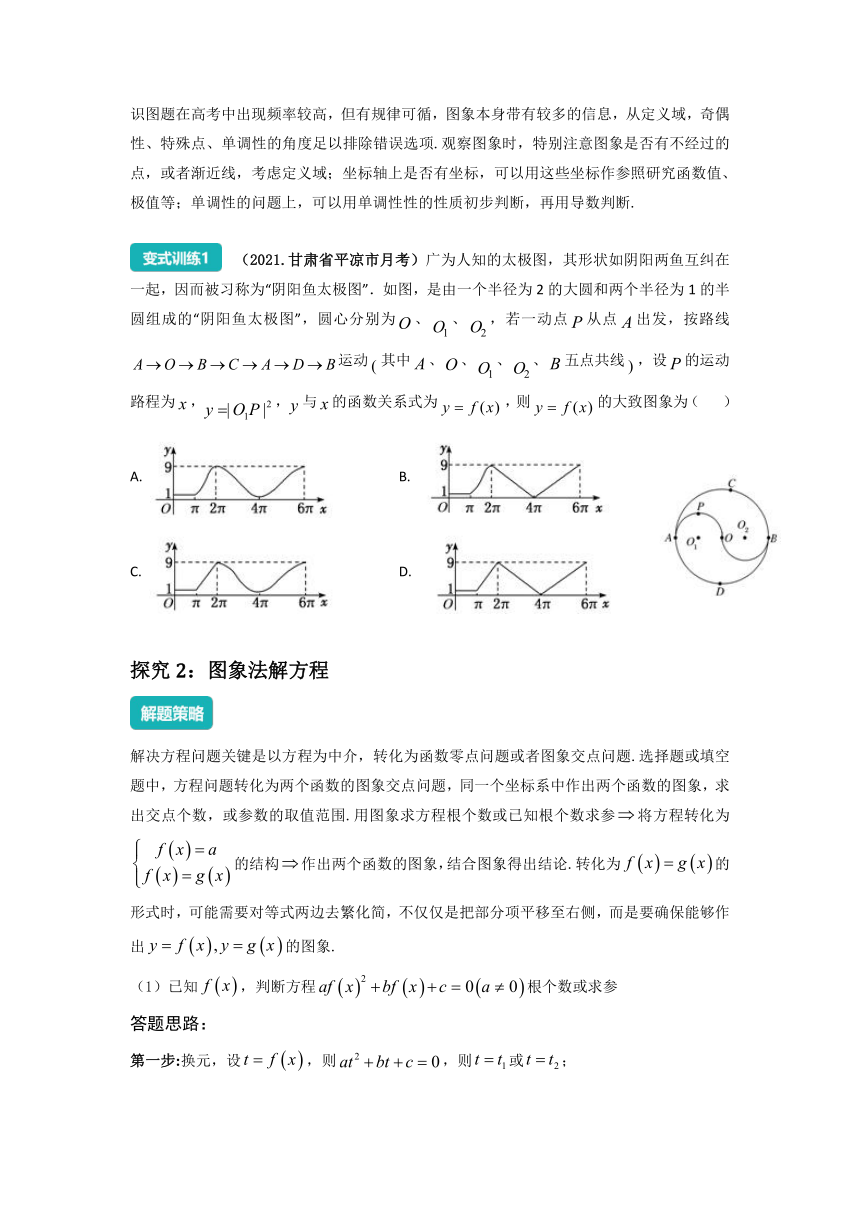
（2021.甘肅省平涼市月考）廣為人知的太極圖，其形狀如陰陽兩魚互糾在一起，因而被習稱為“陰陽魚太極圖”．如圖，是由一個半徑為2的大圓和兩個半徑為1的半圓組成的“陰陽魚太極圖”，圓心分別為、、，若一動點從點出發，按路線運動其中、、、、五點共線，設的運動路程為，，與的函數關系式為，則的大致圖象為（ ）
A. B.
C. D.
探究2：圖象法解方程
解決方程問題關鍵是以方程為中介，轉化為函數零點問題或者圖象交點問題.選擇題或填空題中，方程問題轉化為兩個函數的圖象交點問題，同一個坐標系中作出兩個函數的圖象，求出交點個數，或參數的取值范圍.用圖象求方程根個數或已知根個數求參將方程轉化為的結構作出兩個函數的圖象，結合圖象得出結論.轉化為的形式時，可能需要對等式兩邊去繁化簡，不僅僅是把部分項平移至右側，而是要確保能夠作出的圖象.
（1）已知，判斷方程根個數或求參
答題思路：
第一步:換元，設，則，則或；
第二步: ，轉化為兩條直線與圖象交點問題.
（2）求函數零點個數或已知零點個數求參即為方程根即為函數圖象交點橫坐標；
答題思路：
第一步:轉化為方程轉化為函數圖象交點問題；
第二步:在同一個坐標系中作出兩個函數的圖象；
第三步:結合圖象研究交點個數，若求參數的取值范圍，作出滿足條件的臨界位置的圖象，明確圖象變化范圍，進而求出參數的取值范圍.
(2021.江蘇省蘇州市月考）已知函數，若方程有兩個不同實根，則實數的取值范圍為（ ）
A. B.
C. D.
【審題視點】
題干中出現方程 “有兩個不同實根”，轉化為兩個函數的圖象的交點問題.
【思維引導】
方程轉化為，作出與的圖象，的圖象過定點，找出圖象有兩個交點的臨界位置，求出斜率的取值范圍.
【規范解析】
解：方程有兩個不同實根轉化為：
函數與函數的圖象有兩個不同的交點
當時，，周期性變化，周期為1
函數的圖象恒過點；
作函數與函數的圖象如下，
圖中取，，三點
直線繞點從順時針旋轉，
①當斜率為1時，直線與切于點
此時圖象1個交點，
故當時，函數圖象2個交點
②直線從切線位置繼續旋轉，轉至的過程中，
直線與的圖象2個交點，與函數圖象共3個交點
若繼續順時針旋轉，交點個數超過2個，又
故當時，函數圖象2個交點
綜上：的取值范圍為故選
【探究總結】
題干中已知方程根個數求參問題，把1個方程轉化為2個函數，利用作圖知識，準確的畫出函數圖象，找出臨界位置，求出參數范圍.
(2021.江蘇省蘇州市期中）設函數，若關于的方程恰有6個不同的實數解，則實數的取值范圍為（ ）
A. B. C. D.
探究3：圖象法解不等式
解不等式的思路：
（1）解關于抽象函數的不等式
第一步:結合抽象函數的性質，作出抽象函數的大致圖象；
第二步:結合圖象寫出解集：
① （）圖象在軸的上方或下方的部分對應的的取值范圍；
② 結合函數單調性與奇偶性
若為增函數（減函數），且，則（）；
若在軸右側的圖象單調遞增（減），且，則（）；
③ 結合函數奇偶性變形為結合單調性解不等式.
（2）已知解析式，解不等式（解不等式的思路與的思路一致）
第一步:將不等式，轉化為的形式；
第二步:作出兩個函數的圖象，不等式的解集即為圖象在圖象上方部分對應的的取值范圍.
（3）已知在區間上恒成立，求參數的取值范圍：
第一步: 不等式轉化為或的形式，即函數的圖象恒在的上方或下方；
第二步:①若的圖象為直線或直線翻折得到，作出的圖象，若直線斜率確定，即平移直線；若直線過定點，即直線繞定點旋轉；結合圖象，確定平移或旋轉范圍；
②若與的圖象均為曲線，作出滿足位置關系的圖象；
第三步: ①直線的臨界位置即為與圖象相切的位置，利用導數的幾何意義求解；②比較區間端點處函數值，列出不等式，求參數取值范圍.
(2021.安徽省高三月考）已知函數若不等式對任意的恒成立，則實數的取值范圍是（ ）
A. B. C. D.
【審題視點】
解不等式或不等式恒成立問題，在選擇填空題中首先考慮圖象法，不等式左右兩側對應的函數均為常見函數，其圖象可快速作出.且出現了帶有絕對值的結構，通常選擇圖象法，利用圖象的翻折變換，作出的圖象，解決問題.
【思維引導】
作出的圖象，對于的圖象，可由的圖象平移得到.可先作出的圖象，左右平移確定范圍，臨界位置處兩圖像相切.
【規范解析】
解：作出函數的圖象，如下圖
由不等式對任意的恒成立，
即的圖象不能在的圖象的上方，
①將的圖象向左平移，均滿足
②將的圖象向右平移，平移至與相切的位置處
即為切線，
設切點為，
又，
切點坐標為
綜上可得，的范圍是
故選
【探究總結】
不等式恒成立問題，若通過圖象解決，往往需要對不等式變形，目的是轉化為兩個比較“簡單”的函數，即能用常規的方法作出圖象的函數.若與直線有關，需要研究直線的平移或者旋轉，要與導數幾何意義相結合；若與曲線有關，比較端點處函數值大小.
(2021.江蘇省高三聯考）已知，設關于的不等式的解集為，若，則實數的取值范圍是（ ）
A． B．
C． D．
探究4：圖象與性質的綜合應用
（1）與對稱性結合：
① 已知與的圖象交點坐標為，求或或
：
第一步:在同一坐標系中，作出與的圖象；
第二步: 與有相同的對稱軸或對稱中心，結合圖象，判斷交點的個數；
第三步:結合對稱性，求出每一組對稱點的坐標之和.
② 已知與的圖象上有關于軸（軸或原點）的對稱點，轉化為的圖象關于軸（軸或原點）的對稱函數（或）的圖象與的圖象有交點.
（2）與單調性、奇偶性、周期性的結合：往往結合抽象函數考查
第一步:分析題中抽象函數的性質，作出函數大致圖象或者結合基本初等函數的圖象思考；
第二步:解方程或不等式，轉化為自變量的值之間的關系.
(2021.安徽省高三月考）已知函數的圖像關于直線對稱，則方程的解的個數為（ ）
A. 2 B. 3 C. 4 D. 5
【審題視點】
題中函數為抽象函數，解題時可以先作出大致圖象，結合已知函數圖象幫助理解.抽象函數下的方程問題，要轉化為自變量值之間的等式關系，化抽象為具體，最終轉化為用上述探究二中的方法解決.
【思維引導】
函數關于直線對稱，即函數為偶函數. ，轉化為，即，結合圖象求交點個數，即為方程的根.
【規范解析】
解：由因為函數的圖像關于直線對稱，
可得函數的圖像關于直線對稱，
所以函數為偶函數，
因為，
所以，
令，，
則，
，
兩函數圖像如圖
由圖像可知，兩函數圖像有3個不同的交點，
所以方程的解的個數為3，故答案為
(2021.江蘇省蘇州市模擬）已知是定義在上的奇函數，且，則的最小正周期為___________；若對任意的，當時，都有，則關于x的不等式在區間上的解集為___________.
專題升華
利用函數圖象解題，將抽象問題具體化，是處理函數問題的重要方法，體現數形結合思想、化歸與轉化思想. 而圖象與性質緊密結合，用圖象呈現性質，反之結合性質可作出函數大致圖象.對于圖象的要求是會識圖、作圖、用圖，函數在選擇填空題的考查中，往往會轉化為圖象問題求解，所以掌握常規的作圖方法是關鍵.圖象的考查不僅僅局限與上述的探究方向，利用圖象求函數值域，分析函數性質，求零點個數，方程根個數，求參數的取值范圍等等.因此，函數對圖象要求較高，復習時注意方法思路的總結，能夠以不變應萬變.
【答案詳解】
變式訓練1：
【解析】解：根據題意，用排除法分析：
在區間上，在弧上運動，則
在區間上，在弧運動，此時
則，
則區間上，為增函數且是曲線，排除；
在區間上，在弧運動，此時
則
則區間上，為減函數且是曲線，排除，
故選.
變式訓練2：
【解析】解：作出函數的圖象如圖，
令，則方程轉化為
設方程的兩根為，則，
即與的圖象共6個交點，
由圖象可得，當時，兩直線與的圖象共6個交點
則方程在內有兩不同實數根，
解得，
則實數a的取值范圍為
故選
變式訓練3：
【解析】解： ，
由題意得：在上，函數的圖象應在函數的圖象的下方．
①當時，顯然不滿足條件．
②當時，函數的圖象是把函數的圖象向左平移個單位得到的，函數在上單調遞增，圖象不滿足函數的圖象在函數的圖象下方．
③當時，如圖所示：
在為減，在為增，
的圖象由的圖象向右平移的單位得到，
當時的圖象在的圖象下方，
發現只需當時成立即可滿足條件，
即 ，
結合 化簡得 故，
解得，故此時的范圍為．
綜上可得的范圍為．
故選：．
變式訓練4：
【解析】解：由可得，函數關于對稱，
又函數為奇函數，故函數關于原點對稱，
所以函數的周期為，
因為對任意的，當時，都有，不妨設，所以，所以函數在上是增函數，
所以當時，，
令，設，則，所以是單調遞減函數，
所以當，，
所以當時，，即，由對稱性及周期性作函數的示意圖和的圖象如下圖所示，
則不等式的解集為.
故答案為：2；.

展開更多......

收起↑