資源簡介

專題1.5 空間向量的應用【十大題型】
【人教A版（2019）】
【題型1 求平面的法向量】 2
【題型2 利用空間向量證明線線平行】 3
【題型3 利用空間向量證明線面平行】 5
【題型4 利用空間向量證明面面平行】 7
【題型5 利用空間向量證明線線垂直】 9
【題型6 利用空間向量證明線面垂直】 10
【題型7 利用空間向量證明面面垂直】 12
【題型8 利用空間向量研究距離問題】 15
【題型9 利用空間向量求空間角】 17
【題型10 利用空間向量研究存在性問題】 18
【知識點1 空間中點、直線和平面的向量表示】
1．空間中點、直線和平面的向量表示
(1)空間中點的位置向量：如圖，在空間中，我們取一定點O作為基點，那么空間中任意一點P就可以用向量來表示．我們把向量稱為點P的位置向量．
(2)空間中直線的向量表示式：直線l的方向向量為a ，且過點A.如圖，取定空間中的任意一點O，可以得到點P在直線l上的充要條件是存在實數t，使＝＋ta①，把＝a代入①式得＝＋t②，
①式和②式都稱為空間直線的向量表示式．
(3)平面的法向量定義：
直線l⊥α，取直線l的方向向量a ，我們稱向量a為平面α的法向量.給定一個點A和一個向量a，那么過點A，且以向量a為法向量的平面完全確定，可以表示為集合.
【注】一個平面的法向量不是唯一的，在應用時，可適當取平面的一個法向量.已知一平面內兩條相交直線的方向向量，可求出該平面的一個法向量.
【題型1 求平面的法向量】
【例1】（2023春·高二課時練習）已知，則平面的一個單位法向量是（ ）
A． B．
C． D．
【變式1-1】（2023秋·云南昆明·高二昆明一中校考期末）空間直角坐標系中，已知點，則平面的一個法向量可以是（ ）
A． B． C． D．
【變式1-2】（2023·全國·高二專題練習）如圖，四棱柱的底面是正方形，為底面中心，平面，．平面的法向量為（ ）
A． B． C． D．
【變式1-3】（2023秋·北京石景山·高二統考期末）如圖，在三棱錐中，平面，，以A為原點建立空間直角坐標系，如圖所示，為平面的一個法向量，則的坐標可能是（ ）
A． B． C． D．
【知識點2 用空間向量研究直線、平面的平行關系】
1．空間中直線、平面的平行
(1)線線平行的向量表示：設u1，u2分別是直線l1，l2的方向向量，則l1∥l2 u1∥u2 λ∈R，使得u1＝λu2.
(2)線面平行的向量表示：設u是直線 l 的方向向量，n是平面α的法向量，l α，則l∥α u⊥n u·n＝0.
(3)面面平行的向量表示：設n1 ，n2 分別是平面α，β的法向量，則α∥β n1∥n2 λ∈R，使得n1＝λn2 .
2．利用向量證明線線平行的思路：
證明線線平行只需證明兩條直線的方向向量共線即可．
3．證明線面平行問題的方法：
(1)證明直線的方向向量與平面內的某一向量是共線向量且直線不在平面內；
(2)證明直線的方向向量可以用平面內兩個不共線向量表示且直線不在平面內；
(3)證明直線的方向向量與平面的法向量垂直且直線不在平面內．
4．證明面面平行問題的方法：
(1)利用空間向量證明面面平行，通常是證明兩平面的法向量平行．
(2)將面面平行轉化為線線平行然后用向量共線進行證明．
【題型2 利用空間向量證明線線平行】
【例2】（2023春·高二課時練習）如圖，四邊形ABCD和ABEF都是平行四邊形，且不共面，M，N分別是AC，BF的中點，求證：.
【變式2-1】（2023春·高二課時練習）已知棱長為1的正方體在空間直角坐標系中的位置如圖所示，分別為棱的中點，求證：.
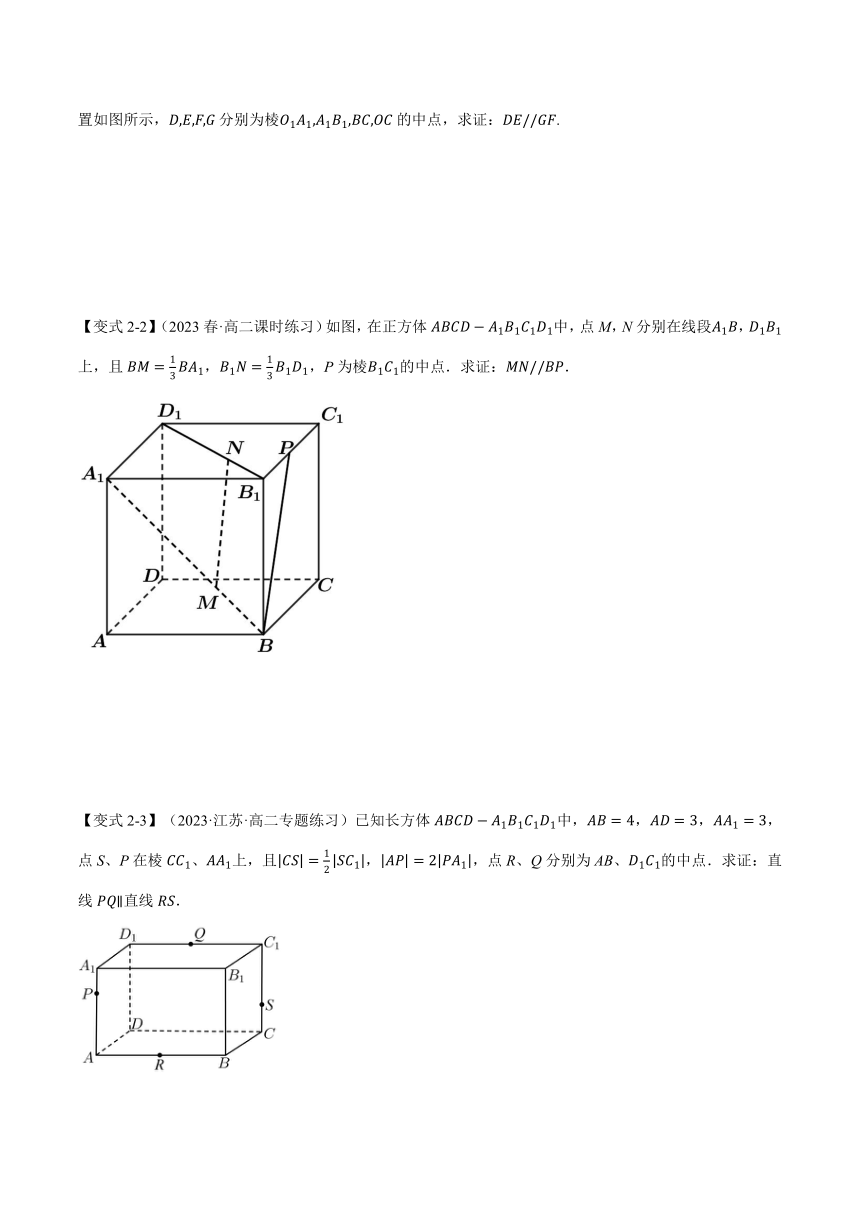
【變式2-2】（2023春·高二課時練習）如圖，在正方體中，點M，N分別在線段，上，且，，P為棱的中點．求證：．
【變式2-3】（2023·江蘇·高二專題練習）已知長方體中，，，，點S、P在棱、上，且，，點R、Q分別為AB、的中點．求證：直線直線．
【題型3 利用空間向量證明線面平行】
【例3】（2023·全國·高二專題練習）如圖，在四棱錐中，底面為直角梯形，其中.平面，且，點在棱上，點為中點.若，證明：直線平面.
【變式3-1】（2023春·高二課時練習）如圖，已知矩形和矩形所在平面互相垂直，點分別在上，且，，求證：平面.
【變式3-2】（2023春·高二課時練習）如圖，在四棱錐P ABCD中，PA⊥底面ABCD，AB⊥AD，BC∥AD，PA=AB=BC=2，AD=4，E為棱PD的中點，（為常數，且）．若直線BF平面ACE，求實數的值；
【變式3-3】（2023·全國·高三專題練習）如圖，在四棱錐中，，，點F為棱CD的中點，與E，F相異的動點P在棱EF上.
(1)當P為EF的中點時，證明：平面ADE；
(2)設平面EAD與平面EBC的交線為l，是否存在點P使得平面PBD？若存在，求的值；若不存在，請說明理由.
【題型4 利用空間向量證明面面平行】
【例4】（2023春·高二課時練習）如圖所示，平面PAD⊥平面ABCD，四邊形ABCD為正方形，△PAD是直角三角形，且PA＝AD＝2，E，F，G分別是線段PA，PD，CD的中點，求證：平面EFG∥平面PBC．
【變式4-1】（2023春·高二課時練習）在正方體中，分別是的中點，試建立適當的空間直角坐標系，求證：平面平面.
【變式4-2】（2023春·高一課時練習）如圖，從所在平面外一點O作向量，，，.求證：
(1)，，，四點共面；
(2)平面平面.
【變式4-3】（2023·江蘇·高二專題練習）已知正方體ABCD-A1B1C1D1的棱長為2，E，F分別是BB1，DD1的中點，
求證：（1）FC1∥平面ADE；
（2）平面ADE∥平面B1C1F.
【知識點3 用空間向量研究直線、平面的垂直關系】
1．空間中直線、平面的垂直
(1)線線垂直的向量表示：設 u1，u2 分別是直線 l1 , l2 的方向向量，則l1⊥l2 u1⊥u2 u1·u2＝0.
(2)線面垂直的向量表示：設u是直線 l 的方向向量，n是平面α的法向量， l α，則l⊥α u∥n λ∈R，使得u＝λn.
(3)面面垂直的向量表示：設n1，n2 分別是平面α，β的法向量，則α⊥β n1⊥n2 n1·n2＝0.
2．證明兩直線垂直的基本步驟：
建立空間直角坐標系→寫出點的坐標→求直線的方向向量→證明向量垂直→得到兩直線垂直．
3．用坐標法證明線面垂直的方法及步驟：
(1)利用線線垂直：①將直線的方向向量用坐標表示；②找出平面內兩條相交直線，并用坐標表示它們的方向向量；③判斷直線的方向向量與平面內兩條直線的方向向量垂直．
(2)利用平面的法向量：①將直線的方向向量用坐標表示；②求出平面的法向量；③判斷直線的方向向量與平面的法向量平行．
4．證明面面垂直的兩種方法：
(1)常規法：利用面面垂直的判定定理轉化為線面垂直、線線垂直去證明．
(2)法向量法：證明兩個平面的法向量互相垂直．
【題型5 利用空間向量證明線線垂直】
【例5】（2023春·高二課時練習）在棱長為1的正方體中，分別是中點，在棱上，，為的中點，求證：；
【變式5-1】（2023秋·廣東廣州·高一校考期中）如圖，，，，，E，F分別是，的中點，M，N分別是，的中點，證明：.
【變式5-2】（2023秋·高二課時練習）如圖，在棱長為1的正方體中，分別是的中點，建立適當的空間直角坐標系，證明：．

【變式5-3】（2023春·高二課時練習）如圖，在四棱錐P-ABCD中，PA⊥平面ABCD，四邊形ABCD是矩形，PA=AB=1，點F是PB的中點，點E在邊BC上移動.求證：無論點E在邊BC上的何處，都有PE⊥AF.
【題型6 利用空間向量證明線面垂直】
【例6】（2023春·高二課時練習）如圖所示，正三棱柱ABC－A1B1C1的所有棱長都為2，D為CC1的中點．求證：AB1⊥平面A1BD.
【變式6-1】（2023春·江蘇宿遷·高二校考階段練習）如圖，已知正方形和矩形所在的平面互相垂直，，，是線段的中點.
(1)求證：.
(2)求證：平面.
【變式6-2】（2023春·廣西柳州·高二校考階段練習）已知平行六面體的所有棱長均為1，．用向量解決下面的問題
(1)求的長；
(2)求證：平面．
【變式6-3】（2023春·高二課時練習）如圖，在四棱錐中，底面，底面為正方形，，E，F分別是的中點.
(1)求證：；
(2)在平面內求一點G，使平面.
【題型7 利用空間向量證明面面垂直】
【例7】（2023春·高二課時練習）如圖所示，△ABC是一個正三角形，EC⊥平面ABC，BD∥CE，且CE＝CA＝2BD，M是EA的中點．求證：平面DEA⊥平面ECA.
【變式7-1】（2023·全國·高三專題練習）如圖，在五面體ABCDEF中，FA⊥平面ABCD，，若 .
(1)求五面體ABCDEF的體積；
(2)若M為EC的中點，求證：平面平面AMD.
【變式7-2】（2023秋·新疆昌吉·高二校考期末）如圖，在四棱錐P－ABCD中，PA⊥底面ABCD，AD⊥AB，AB∥DC，AD＝DC＝AP＝2，AB＝1，點E為棱PC的中點．證明：
(1)BE∥平面PAD；
(2)平面PCD⊥平面PAD．
【變式7-3】（2023·全國·高三專題練習）如圖，在三棱錐P-ABC中， ，D是BC的中點，PO⊥平面ABC，垂足O落在線段AD上，已知 ．
(1)求證：AP⊥BC；
(2)若點M是線段AP是一點，且 ．試證明平面AMC⊥平面BMC．
【知識點4 用空間向量研究距離、夾角問題】
1．距離問題
(1)點P到直線 l 的距離：已知直線l的單位方向向量為u，A是直線l上的定點，P是直線l外一點，設向量在直線l上的投影向量為＝a，則點P到直線l的距離為 (如圖)．
(2)點P到平面α的距離：設平面α的法向量為n，A是平面α內的定點，P是平面α外一點，則點P到平面α的距離為(如圖)．
2．夾角問題
(1)兩個平面的夾角：平面α與平面β的夾角：平面α與平面β相交，形成四個二面角，我們把這四個二面角中不大于90° 的二面角稱為平面α與平面β的夾角．
(2)空間角的向量法解法
角的分類 向量求法 范圍
兩條異面直線所成的角 設兩異面直線 l1，l2 所成的角為θ，其方向向量分別為u，v，則cos θ＝|cos〈u，v〉|＝
直線與平面所成的角 設直線AB與平面α所成的角為θ，直線AB的方向向量為u，平面α的法向量為n，則sin θ＝|cos 〈u，n〉|＝
兩個平面的夾角 設平面α與平面β的夾角為θ，平面α，β的法向量分別為n1，n2，則cos θ＝|cos 〈n1，n2〉|＝
【題型8 利用空間向量研究距離問題】
【例8】（2023·全國·高三專題練習）如圖，直四棱柱的底面為平行四邊形，，，點P，M分別為，上靠近的三等分點．
(1)求點M到直線的距離；
(2)求直線PD與平面所成角的正弦值.
【變式8-1】（2023春·浙江溫州·高二校聯考期末）如圖所示，在棱長為1的正方體中為線段的中點.

(1)求證：平面平面；
(2)求到平面的距離.
【變式8-2】（2023春·高二課時練習）直四棱柱中，底面為正方形，邊長為，側棱，分別為的中點，分別是的中點．

(1)求證：平面 平面；
(2)求平面與平面的距離．
【變式8-3】（2023春·高二課時練習）如圖，在長方體中，，，求：
(1)點到直線BD的距離；
(2)點到平面的距離；
(3)異面直線之間的距離.
【題型9 利用空間向量求空間角】
【例9】（2023春·湖北荊門·高二統考期末）如圖，三棱柱中，面面，，，．過的平面交線段于點（不與端點重合），交線段于點．

(1)求證：四邊形為平行四邊形；
(2)若，求直線與平面所成角的正弦值．
【變式9-1】（2023春·陜西西安·高一校考期末）如圖1，在中，，，，，都在上，且，，將，分別沿，折起，使得點，在點處重合，得到四棱錐，如圖2.

(1)求異面直線，所成角的余弦值；
(2)若為的中點，求鈍二面角的余弦值.
【變式9-2】（2023春·湖南衡陽·高二統考期末）如圖，在四棱錐中，四邊形是矩形，平面（垂足H在矩形內），E為棱的中點，平面.

(1)證明：；
(2)若，直線PC與平面所成角為，求平面與平面夾角的余弦值.
【變式9-3】（2023春·江蘇連云港·高二統考期中）如圖，在四棱錐中，平面，與底面所成的角為45°，底面為直角梯形，，，．

(1)求直線與平面所成角的正弦值；
(2)求平面與平面所成的銳二面角的余弦值．
【題型10 利用空間向量研究存在性問題】
【例10】（2023·全國·高三對口高考）如圖所示的幾何體中，四邊形是等腰梯形，，，平面，，.

(1)求二面角的余弦值；
(2)在線段AB（含端點）上，是否存在一點P，使得平面.若存在，求出的值；若不存在，請說明理由.
【變式10-1】（2023·湖北襄陽·校考模擬預測）在三棱錐P-ABC中，若已知，，點P在底面ABC的射影為點H，則
(1)證明：
(2)設，則在線段PC上是否存在一點M，使得與平面所成角的余弦值為，若存在，設，求出的值，若不存在，請說明理由.
【變式10-2】（2023·河北衡水·河北校考三模）圖1是直角梯形ABCD，，∠D＝90°，四邊形ABCE是邊長為2的菱形，并且∠BCE＝60°，以BE為折痕將△BCE折起，使點C到達的位置，且．
(1)求證：平面平面ABED．
(2)在棱上是否存在點P，使得點P到平面的距離為？若存在，求出直線EP與平面所成角的正弦值；若不存在，請說明理由．
【變式10-3】（2023春·廣東佛山·高二校考階段練習）如圖，在四棱錐中，已知底面是正方形，底面，且，是棱上動點.
(1)證明：平面.
(2)線段上是否存在點，使二面角的余弦值是？若存在，求的值；若不存在，請說明理由.
專題1.5 空間向量的應用【十大題型】
【人教A版（2019）】
【題型1 求平面的法向量】 2
【題型2 利用空間向量證明線線平行】 5
【題型3 利用空間向量證明線面平行】 7
【題型4 利用空間向量證明面面平行】 12
【題型5 利用空間向量證明線線垂直】 17
【題型6 利用空間向量證明線面垂直】 20
【題型7 利用空間向量證明面面垂直】 24
【題型8 利用空間向量研究距離問題】 30
【題型9 利用空間向量求空間角】 36
【題型10 利用空間向量研究存在性問題】 41
【知識點1 空間中點、直線和平面的向量表示】
1．空間中點、直線和平面的向量表示
(1)空間中點的位置向量：如圖，在空間中，我們取一定點O作為基點，那么空間中任意一點P就可以用向量來表示．我們把向量稱為點P的位置向量．
(2)空間中直線的向量表示式：直線l的方向向量為a ，且過點A.如圖，取定空間中的任意一點O，可以得到點P在直線l上的充要條件是存在實數t，使＝＋ta①，把＝a代入①式得＝＋t②，
①式和②式都稱為空間直線的向量表示式．
(3)平面的法向量定義：
直線l⊥α，取直線l的方向向量a ，我們稱向量a為平面α的法向量.給定一個點A和一個向量a，那么過點A，且以向量a為法向量的平面完全確定，可以表示為集合.
【注】一個平面的法向量不是唯一的，在應用時，可適當取平面的一個法向量.已知一平面內兩條相交直線的方向向量，可求出該平面的一個法向量.
【題型1 求平面的法向量】
【例1】（2023春·高二課時練習）已知，則平面的一個單位法向量是（ ）
A． B．
C． D．
【解題思路】待定系數法設平面的一個法向量為，由法向量的性質建立方程組解出分析即可.
【解題思路】設平面的一個法向量為，
又，
由，
即，
又因為單位向量的模為1，所以B選項正確，
故選：B.
【變式1-1】（2023秋·云南昆明·高二昆明一中校考期末）空間直角坐標系中，已知點，則平面的一個法向量可以是（ ）
A． B． C． D．
【解題思路】根據法向量的求解方法求解即可.
【解題思路】解：由題知，
設平面的一個法向量為，
所以，即，令得
所以，平面的一個法向量可以是.
故選：A.
【變式1-2】（2023·全國·高二專題練習）如圖，四棱柱的底面是正方形，為底面中心，平面，．平面的法向量為（ ）
A． B． C． D．
【解題思路】根據空間直角坐標系寫出各向量，利用法向量的性質可得解.
【解題思路】是正方形，且，
，
，
，，，，
，，
又，
，，
平面的法向量為，
則，得，，
結合選項，可得，
故選：C.
【變式1-3】（2023秋·北京石景山·高二統考期末）如圖，在三棱錐中，平面，，以A為原點建立空間直角坐標系，如圖所示，為平面的一個法向量，則的坐標可能是（ ）
A． B． C． D．
【解題思路】先求出，根據法向量求解公式列方程即可求解．
【解題思路】依題意得，，則
設，則
，取則，所以
故選：D.
【知識點2 用空間向量研究直線、平面的平行關系】
1．空間中直線、平面的平行
(1)線線平行的向量表示：設u1，u2分別是直線l1，l2的方向向量，則l1∥l2 u1∥u2 λ∈R，使得u1＝λu2.
(2)線面平行的向量表示：設u是直線 l 的方向向量，n是平面α的法向量，l α，則l∥α u⊥n u·n＝0.
(3)面面平行的向量表示：設n1 ，n2 分別是平面α，β的法向量，則α∥β n1∥n2 λ∈R，使得n1＝λn2 .
2．利用向量證明線線平行的思路：
證明線線平行只需證明兩條直線的方向向量共線即可．
3．證明線面平行問題的方法：
(1)證明直線的方向向量與平面內的某一向量是共線向量且直線不在平面內；
(2)證明直線的方向向量可以用平面內兩個不共線向量表示且直線不在平面內；
(3)證明直線的方向向量與平面的法向量垂直且直線不在平面內．
4．證明面面平行問題的方法：
(1)利用空間向量證明面面平行，通常是證明兩平面的法向量平行．
(2)將面面平行轉化為線線平行然后用向量共線進行證明．
【題型2 利用空間向量證明線線平行】
【例2】（2023春·高二課時練習）如圖，四邊形ABCD和ABEF都是平行四邊形，且不共面，M，N分別是AC，BF的中點，求證：.
【解題思路】根據給定條件，利用空間向量的線性運算，計算判斷與共線即可推理作答.
【解題思路】（方法1）因為M，N分別是AC，BF的中點，且四邊形ABCD和ABEF都是平行四邊形，
則有，又，
兩式相加得：，因此與共線，而直線與不重合，
所以.
（方法2）因為M，N分別是AC，BF的中點，且四邊形ABCD和ABEF都是平行四邊形，
，
因此與共線，而直線與不重合，
所以.
【變式2-1】（2023春·高二課時練習）已知棱長為1的正方體在空間直角坐標系中的位置如圖所示，分別為棱的中點，求證：.
【解題思路】由圖中的空間直角坐標系，求出相關點的坐標，證明，可得.
【解題思路】因為正方體的棱長為1， 分別為棱的中點，
所以有， ， ， ，
所以，，則有，所以.
【變式2-2】（2023春·高二課時練習）如圖，在正方體中，點M，N分別在線段，上，且，，P為棱的中點．求證：．
【解題思路】利用空間向量共線定理證明.
【解題思路】證明：．
因為，，
所以，
，
．
又因為P為中點，
所以，
從而與為共線向量．
因為直線MN與BP不重合，
所以．
【變式2-3】（2023·江蘇·高二專題練習）已知長方體中，，，，點S、P在棱、上，且，，點R、Q分別為AB、的中點．求證：直線直線．
【解題思路】利用坐標法，利用向量共線定理即得.
【解題思路】以點D為原點，分別以、與的方向為x、y與z軸的正方向，建立空間直角坐標系．
則、、、、、、、，
由題意知、、、，
∴，．
∴，又，不共線，
∴.
【題型3 利用空間向量證明線面平行】
【例3】（2023·全國·高二專題練習）如圖，在四棱錐中，底面為直角梯形，其中.平面，且，點在棱上，點為中點.若，證明：直線平面.
【解題思路】建立空間直角坐標系，利用空間向量法證明即可.
【解題思路】如圖所示，以點為坐標原點，以為軸，為軸，為軸建立空間直角坐標系，
則，
若，則，，
因為平面，平面，所以，
又因為，，平面，
所以平面
平面的其中一個法向量為，
所以，即，
又因為平面，
所以平面.
【變式3-1】（2023春·高二課時練習）如圖，已知矩形和矩形所在平面互相垂直，點分別在上，且，，求證：平面.
【解題思路】根據已知條件建立空間直角坐標系，寫出相關點的坐標，求出直線的方向向量和平面的法向量，利用直線與平面平行的直線的方向向量與平面的法向量的關系即可求解.
【解題思路】因為矩形和矩形所在平面互相垂直，所以互相垂直．
不妨設的長分別為，以為正交基底，建立空間直角坐標系如圖所示，
則， ， ， ，
所以.
因為，，
所以.
又平面的一個法向量是
由,得.
因為平面，
所以平面.
【變式3-2】（2023春·高二課時練習）如圖，在四棱錐P ABCD中，PA⊥底面ABCD，AB⊥AD，BC∥AD，PA=AB=BC=2，AD=4，E為棱PD的中點，（為常數，且）．若直線BF平面ACE，求實數的值；
【解題思路】由題意可知，，，兩兩垂直，建立如圖所示的空間直角坐標系，分別求出平面ACE的法向量和直線BF的方向向量，由，即可得出答案.
【解題思路】因為底面，，平面，所以，．
由題意可知，，，兩兩垂直，建立如圖所示的空間直角坐標系，
則，，，，，，
所以，，，，
則，所以．
設平面的一個法向量為．
由得：不妨令，得．
因為平面，所以，解得．
【變式3-3】（2023·全國·高三專題練習）如圖，在四棱錐中，，，點F為棱CD的中點，與E，F相異的動點P在棱EF上.
(1)當P為EF的中點時，證明：平面ADE；
(2)設平面EAD與平面EBC的交線為l，是否存在點P使得平面PBD？若存在，求的值；若不存在，請說明理由.
【解題思路】（1）設點為棱的中點，連接，，通過證明四邊形為平行四邊形，得到，再根據線面平行的判定定理可證平面ADE；
（2）延長，相交于點，連接，則直線為平面與平面的交線，連接，交于點，若平面，由線面平行的性質可知，設，推出，根據三點共線的結論求出，從而可推出.
【解題思路】（1）
如圖，設點為棱的中點，連接，，
∴,，
∵，，
∴，，
∴四邊形為平行四邊形，
∴，
又平面，平面，
∴平面.
（2）
如圖，延長，相交于點，連接，則直線為平面與平面的交線，連接，交于點，
若平面，由線面平行的性質可知，
設，
∵點為棱的中點，，，
∴ ，
∵，，三點共線，
∴，即，
所以當時，，∴，
又平面，平面，∴平面，
∴存在滿足條件的點使得平面，此時.
【題型4 利用空間向量證明面面平行】
【例4】（2023春·高二課時練習）如圖所示，平面PAD⊥平面ABCD，四邊形ABCD為正方形，△PAD是直角三角形，且PA＝AD＝2，E，F，G分別是線段PA，PD，CD的中點，求證：平面EFG∥平面PBC．
【解題思路】根據題意得到AB，AP，AD兩兩垂直，從而以A為坐標原點，AB，AD，AP所在直線分別為x軸，y軸，z軸，建立空間直角坐標系，并確定A，B，C，D，P，E，F，G的坐標，求得，，，，從而即可確定平面EFG的法向量，平面PBC的法向量，進而即可證明平面EFG∥平面PBC．
【解題思路】因為平面PAD⊥平面ABCD，四邊形ABCD為正方形，△PAD是直角三角形，
所以AB，AP，AD兩兩垂直，
以A為坐標原點，AB，AD，AP所在直線分別為x軸，y軸，z軸，建立空間直角坐標系，
則A(0，0，0)，B(2，0，0)，C(2，2，0)，D(0，2，0)，P(0，0，2)，E(0，0，1)，F(0，1，1)，G(1，2，0)．
所以，，，，
設是平面EFG的法向量，
則，，即，得，
令，則，，所以，
設是平面PBC的法向量，
由，，即，得，
令，則，，所以，
所以，所以平面EFG∥平面PBC．
【變式4-1】（2023春·高二課時練習）在正方體中，分別是的中點，試建立適當的空間直角坐標系，求證：平面平面.
【解題思路】根據正方體的結構特征，以為坐標原點建立空間直角坐標系，利用向量的坐標運算證明線線平行，由面面平行的判定定理證明平面平面.
【解題思路】證明:　如圖，以為坐標原點，所在直線分別為x軸、y軸、z軸，
建立空間直角坐標系．設正方體的棱長為1，
則有，，， ， ， ，
于是， ，，，
顯然有，，所以，，
由，平面，平面，平面，
同理平面， 平面，，
所以平面平面.
【變式4-2】（2023春·高一課時練習）如圖，從所在平面外一點O作向量，，，.求證：
(1)，，，四點共面；
(2)平面平面.
【解題思路】（1）利用共面向量定理證明，由可得四點共面；
（2）利用共線向量定理，可得： ， ，從而利用面面平行的判定定理即可證明.
【解題思路】（1）證明：因為從所在平面外一點O作向量，，，，
所以，
所以
，
故，，，四點共面，證畢.
（2）證明：，從而 ，
∵平面，平面，
∴平面，
由（1）知 ，
∵平面，平面，
∴平面，
因為，平面，
所以平面平面.
【變式4-3】（2023·江蘇·高二專題練習）已知正方體ABCD-A1B1C1D1的棱長為2，E，F分別是BB1，DD1的中點，
求證：（1）FC1∥平面ADE；
（2）平面ADE∥平面B1C1F.
【解題思路】（1）建立空間直角坐標系，寫出點的坐標，求得直線的方向向量以及平面的法向量，計算其數量積即可證明；
（2）計算兩個平面的法向量，根據法向量是否平行，即可證明.
【解題思路】證明：如圖，建立空間直角坐標系D-xyz，
則D(0，0，0)，A(2，0，0)，C(0，2，0)，C1(0，2，2)，
E(2，2，1)，F(0，0，1)，B1(2，2，2)，
所以=(0，2，1)，=(2，0，0)，=(0，2，1).
（1）設=(x1，y1，z1)是平面ADE的法向量，則⊥，⊥，
即得令z1=2，則y1=-1，
所以=(0，-1，2).因為·=-2+2=0，所以 .
又因為FC1 平面ADE，所以FC1∥平面ADE.
（2）=(2，0，0).
設=(x2，y2，z2)是平面B1C1F的一個法向量.由⊥，⊥，
得
令z2=2，則y2=-1，所以=(0，-1，2).
因為=，所以平面ADE∥平面B1C1F.
【知識點3 用空間向量研究直線、平面的垂直關系】
1．空間中直線、平面的垂直
(1)線線垂直的向量表示：設 u1，u2 分別是直線 l1 , l2 的方向向量，則l1⊥l2 u1⊥u2 u1·u2＝0.
(2)線面垂直的向量表示：設u是直線 l 的方向向量，n是平面α的法向量， l α，則l⊥α u∥n λ∈R，使得u＝λn.
(3)面面垂直的向量表示：設n1，n2 分別是平面α，β的法向量，則α⊥β n1⊥n2 n1·n2＝0.
2．證明兩直線垂直的基本步驟：
建立空間直角坐標系→寫出點的坐標→求直線的方向向量→證明向量垂直→得到兩直線垂直．
3．用坐標法證明線面垂直的方法及步驟：
(1)利用線線垂直：①將直線的方向向量用坐標表示；②找出平面內兩條相交直線，并用坐標表示它們的方向向量；③判斷直線的方向向量與平面內兩條直線的方向向量垂直．
(2)利用平面的法向量：①將直線的方向向量用坐標表示；②求出平面的法向量；③判斷直線的方向向量與平面的法向量平行．
4．證明面面垂直的兩種方法：
(1)常規法：利用面面垂直的判定定理轉化為線面垂直、線線垂直去證明．
(2)法向量法：證明兩個平面的法向量互相垂直．
【題型5 利用空間向量證明線線垂直】
【例5】（2023春·高二課時練習）在棱長為1的正方體中，分別是中點，在棱上，，為的中點，求證：；
【解題思路】設，則，，，計算得到證明.
【解題思路】設，則，
，
，
，
，故.
【變式5-1】（2023秋·廣東廣州·高一校考期中）如圖，，，，，E，F分別是，的中點，M，N分別是，的中點，證明：.
【解題思路】由題意，利用向量法，根據空間向量的基本定理，結合數量積證明垂直，可得答案.
【解題思路】由題意，連接，如下圖：
，
同理，
故
由，，，，則，
故.
【變式5-2】（2023秋·高二課時練習）如圖，在棱長為1的正方體中，分別是的中點，建立適當的空間直角坐標系，證明：．

【解題思路】建立空間直角坐標系，寫出的坐標，利用空間向量垂直的坐標表示證明即可.
【解題思路】證明：以為坐標原點，分別為軸建立空間直角坐標系，如圖所示：

因為正方體棱長為1，分別是的中點，
所以，
所以，
所以，
由，
所以，
即.
【變式5-3】（2023春·高二課時練習）如圖，在四棱錐P-ABCD中，PA⊥平面ABCD，四邊形ABCD是矩形，PA=AB=1，點F是PB的中點，點E在邊BC上移動.求證：無論點E在邊BC上的何處，都有PE⊥AF.
【解題思路】本題建立空間直角坐標系，求出兩直線的方向向量，求數量積即可判斷.
【解題思路】證明：(方法1)以A為原點，以AD，AB，AP所在直線分別為x軸，y軸，z軸建立空間直角坐標系，設AD=a，
則A(0，0，0)，P(0，0，1)，B(0，1，0)，C(a，1，0)，
于是F.
∵E在BC上，∴設E(m，1，0)，∴=(m，1，-1)，.
∵=0，∴PE⊥AF.
∴無論點E在邊BC上何處，總有PE⊥AF.
(方法2)因為點E在邊BC上，可設=λ，
于是=()·)=+λ)·()
=+λ+λ)=(0-1+1+0+0+0)=0，
因此.
故無論點E在邊BC上的何處，都有PE⊥AF.
【題型6 利用空間向量證明線面垂直】
【例6】（2023春·高二課時練習）如圖所示，正三棱柱ABC－A1B1C1的所有棱長都為2，D為CC1的中點．求證：AB1⊥平面A1BD.
【解題思路】建系，利用空間向量證明線面垂直.
【解題思路】如圖所示，取BC的中點O，連接AO，因為△ABC為正三角形，
所以AO⊥BC，
因為在正三棱柱ABC－A1B1C1中，CC1⊥平面ABC，
平面ABC，則，
，平面BCC1B1，
所以AO⊥平面BCC1B1，
取B1C1的中點O1，以O為坐標原點，
以分別為x軸、y軸、z軸的正方向建立空間直角坐標系，
則，
所以，
則，
可得，即AB1⊥BA1，AB1⊥BD，
BA1∩BD＝B，平面，
所以AB1⊥平面A1BD.
【變式6-1】（2023春·江蘇宿遷·高二校考階段練習）如圖，已知正方形和矩形所在的平面互相垂直，，，是線段的中點.
(1)求證：.
(2)求證：平面.
【解題思路】（1）利用面面垂直性質定理證明平面，然后以點為坐標原點建立空間直角坐標系，利用空間向量坐標法證明線線垂直；
（2）先求出平面的法向量，然后利用直線AM的方向向量與法向量共線即可證明線面垂直.
【解題思路】（1）因為四邊形為矩形，則，
因為平面平面，平面平面，平面，
所以平面，又四邊形為正方形，
以點為坐標原點，、、所在直線分別為、、軸，
建立空間直角坐標系，
由，，得，，，，
，，.
所以，，
所以，所以，
所以
（2）由（1）知，，，.
設是平面的法向量，則，，
所以，得，
取，得，，則.
因為，所以，即與共線.
所以平面.
【變式6-2】（2023春·廣西柳州·高二校考階段練習）已知平行六面體的所有棱長均為1，．用向量解決下面的問題
(1)求的長；
(2)求證：平面．
【解題思路】（1）利用轉化法將換成，利用求模長即可；
（2）利用向量垂直來證明，，再利用線面垂直的判定定理證明即可.
【解題思路】（1）設，
則，
又，
所以
，
即；
（2）因為，
所以
．
所以，同理可得，
又平面．
所以平面．
【變式6-3】（2023春·高二課時練習）如圖，在四棱錐中，底面，底面為正方形，，E，F分別是的中點.
(1)求證：；
(2)在平面內求一點G，使平面.
【解題思路】（1）建立空間直角坐標系，設，寫出各點坐標，求得向量，由即得；
（2）設，求出平面內兩個不共線向量，由和求得確定點位置．
【解題思路】（1）因為底面，平面，平面，
所以，，又底面為正方形，
所以，
以D為原點，分別以DA，DC，DP所在直線為x軸、y軸、z軸建立空間直角坐標系，
設，則D(0，0，0)，A(a，0，0)，B(a，a，0)，C(0，a，0)，E，P(0，0，a)，F，
∴，，
∴＝0，
∴，即EF⊥CD；
（2）設，則，，，
若使GF⊥平面PCB，則需且，
由，
解得，
由 ，
解得，
因為為平面內兩條相交直線，故平面，
∴G點坐標為，即G為AD的中點．
【題型7 利用空間向量證明面面垂直】
【例7】（2023春·高二課時練習）如圖所示，△ABC是一個正三角形，EC⊥平面ABC，BD∥CE，且CE＝CA＝2BD，M是EA的中點．求證：平面DEA⊥平面ECA.
【解題思路】建系，分別求平面DEA、平面ECA的法向量，利用空間向量證明面面垂直.
【解題思路】建立如圖所示的空間直角坐標系C－xyz，不妨設CA＝2，則CE＝2，BD＝1，
則，
所以，
設平面ECA的一個法向量是，
則，
取，則，即，
設平面DEA的一個法向量是，
則，
取，則，即，
因為，所以，
所以平面DEA⊥平面ECA.
【變式7-1】（2023·全國·高三專題練習）如圖，在五面體ABCDEF中，FA⊥平面ABCD，，若 .
(1)求五面體ABCDEF的體積；
(2)若M為EC的中點，求證：平面平面AMD.
【解題思路】（1）取AD中點N，連接EN，，易證得EN⊥平面ABCD，五面體的體積棱柱的體積棱錐的體積，分別求出棱柱的體積和棱錐的體積即可得出答案.
（2）證法1：以A為坐標原點，以，，為軸正半軸建立空間直角坐標系.由垂直向量的坐標運算可證得，即可得出CE⊥平面AMD，再由面面垂直的判定定理即可證明；證法2：由題意證得，即可得出CE⊥平面AMD，再由面面垂直的判定定理即可證明；
【解題思路】（1）因為，取AD中點N，連接EN，，
因為，所以，
又FA⊥平面ABCD，平面ABCD，，
所以EN⊥平面ABCD，又因為，即，，
平面，所以平面，
所以為底面是等腰直角三角形的直棱柱，
高等于1，三棱錐是高等于1底面是等腰直角三角形.
五面體的體積棱柱的體積棱錐的體積.
即：
（2）證法1：以A為坐標原點，以，，為軸正半軸建立空間直角坐標系.
點，，，，
所以
得到：
所以，，平面AMD，
所以CE⊥平面AMD，又CE平面CDE，所以平面平面AMD.
證法2：因為，所以為等腰三角形，M為EC的中點，所以；
同理在中，，（N為AD中點）又AM、MN平面AMD，
，所以CE⊥平面AMD，又CE平面CDE，
平面⊥平面AMD.
【變式7-2】（2023秋·新疆昌吉·高二校考期末）如圖，在四棱錐P－ABCD中，PA⊥底面ABCD，AD⊥AB，AB∥DC，AD＝DC＝AP＝2，AB＝1，點E為棱PC的中點．證明：
(1)BE∥平面PAD；
(2)平面PCD⊥平面PAD．
【解題思路】（1）根據題意，先證明AB，AD，AP兩兩垂直，從而建立對應的空間直角坐標系，再利用空間向量法證明平面PAD的一個法向量與垂直，進而即可證明結論；
（2）結合（1），先證明平面PCD的一個法向量與平面PAD的一個法向量垂直，進而即可證明結論．
【解題思路】（1）因為PA⊥平面ABCD，且AB 平面ABCD，所以AB⊥PA，
又因為AB⊥AD，且PA∩AD＝A，PA，平面PAD，所以AB⊥平面PAD，
依題意，以點A為原點，以AB，AD，AP分別為x，y，z軸建立如圖所示的空間直角坐標系，
則B(1,0,0)，C(2,2,0)，D(0,2,0)，P(0,0,2)，
由E為棱PC的中點，得E(1,1,1)，則，
所以為平面PAD的一個法向量，
又，所以BE⊥AB，
又平面PAD，所以BE∥平面PAD．
（2）由（1）知平面PAD的法向量，，，
設平面PCD的一個法向量為，
則，即，令y＝1，可得z＝1，所以，
又，
所以，所以平面PAD⊥平面PCD．
【變式7-3】（2023·全國·高三專題練習）如圖，在三棱錐P-ABC中， ，D是BC的中點，PO⊥平面ABC，垂足O落在線段AD上，已知 ．
(1)求證：AP⊥BC；
(2)若點M是線段AP是一點，且 ．試證明平面AMC⊥平面BMC．
【解題思路】（1）建立空間直角坐標系，求出相關點坐標，求出向量的坐標，計算，即可證明結論；
（2）求出平面平面AMC和平面BMC的法向量，計算法向量的數量積，結果為0，即可證明結論.
【解題思路】（1）
證明：以O為原點，過點O作CB的平行線為x軸，以AD方向為y軸正方向，以射線OP的方向為Z軸正方向，建立空間直角坐標系，如圖所示；
則 ，
故，，
∴，
∴⊥，即 ；
（2）
證明：因為 平面ABC，平面ABC，所以,
因為 ，故 ，∵M為AP上一點，且 ，
∴M(0,，)，∴(0,,)，
(-4,,)，(4,,)；
設平面BMC的法向量為，
則 ，即，
令 ，則 ；
設平面AMC的法向量為，則 ，
即，令 ，則；
由于，
得⊥，即平面AMC⊥平面BMC．
【知識點4 用空間向量研究距離、夾角問題】
1．距離問題
(1)點P到直線 l 的距離：已知直線l的單位方向向量為u，A是直線l上的定點，P是直線l外一點，設向量在直線l上的投影向量為＝a，則點P到直線l的距離為 (如圖)．
(2)點P到平面α的距離：設平面α的法向量為n，A是平面α內的定點，P是平面α外一點，則點P到平面α的距離為(如圖)．
2．夾角問題
(1)兩個平面的夾角：平面α與平面β的夾角：平面α與平面β相交，形成四個二面角，我們把這四個二面角中不大于90° 的二面角稱為平面α與平面β的夾角．
(2)空間角的向量法解法
角的分類 向量求法 范圍
兩條異面直線所成的角 設兩異面直線 l1，l2 所成的角為θ，其方向向量分別為u，v，則cos θ＝|cos〈u，v〉|＝
直線與平面所成的角 設直線AB與平面α所成的角為θ，直線AB的方向向量為u，平面α的法向量為n，則sin θ＝|cos 〈u，n〉|＝
兩個平面的夾角 設平面α與平面β的夾角為θ，平面α，β的法向量分別為n1，n2，則cos θ＝|cos 〈n1，n2〉|＝
【題型8 利用空間向量研究距離問題】
【例8】（2023·全國·高三專題練習）如圖，直四棱柱的底面為平行四邊形，，，點P，M分別為，上靠近的三等分點．
(1)求點M到直線的距離；
(2)求直線PD與平面所成角的正弦值.
【解題思路】（1）建立空間直角坐標系，寫出相應點的坐標，利用向量法求出點到直線的距離即可；
（2）結合（1）中點的坐標，分別求出直線的方向向量和平面的法向量，利用空間向量的夾角公式即可求解.
【解題思路】（1）由題可得AD=2，，
又點P為AB上靠近A的三等分點，所以AP=1．
在中，由余弦定理可得，
，
故，
所以為直角三角形，故DP⊥AB．
因為底面ABCD為平行四邊形，所以DP⊥CD．
由直四棱柱性質可知，，
即DP，CD，兩兩垂直．
故以D為坐標原點，分別以DP，DC，所在直線為x軸，y軸，z軸，建立如圖所示的空間直角坐標系Dxyz．
則．
因為，過點M作，（點到直線的距離即為通過該點向直線做垂線，點到垂足的距離）
令，所以，故．
由，解得，所以，故點M到直線的距離為．
（2）因為，，，
設平面的法向量為，則即
令，得，，故．
設直線PD與平面所成角為，
則．
所以直線PD與平面所成角的正弦值為．
【變式8-1】（2023春·浙江溫州·高二校聯考期末）如圖所示，在棱長為1的正方體中為線段的中點.

(1)求證：平面平面；
(2)求到平面的距離.
【解題思路】（1）先證線面垂直，再根據面面垂直的判定定理可證結論；
（2）建立坐標系，結合空間向量，利用點到平面的距離公式可求答案.
【解題思路】（1）因為是正方體，所以平面，所以.
又，，所以平面，
平面，所以平面平面.
（2）在正方體中，以為原點，建立空間直角坐標系如圖所示，則，，，，，，，設平面的一個法向量為，.
由令，則，，即.
設到平面的距離為，則，即點到平面的距離為.
【變式8-2】（2023春·高二課時練習）直四棱柱中，底面為正方形，邊長為，側棱，分別為的中點，分別是的中點．

(1)求證：平面 平面；
(2)求平面與平面的距離．
【解題思路】（1）法一：由面面平行的判定定理即可證明；法二：如圖所示，建立空間直角坐標系，通過證明，再由面面平行的判定定理即可證明.
（2）法一: 平面與平面的距離到平面的距離,再由等體積法即可求出答案. 法二:求出平面的法向量,，平面與平面的距離等于到平面的距離，由點到平面的距離公式即可求出答案.
【解題思路】（1）法一:證明：連接分別為的中點，
分別是的中點，
，平面，平面，
平面，平行且等于，
是平行四邊形，，
平面，平面，平面，
，平面平面；
法二: 如圖所示，建立空間直角坐標系，
則，
，
，
，，，
平面，平面，平面，
平面，平面，平面，
又，平面平面，
（2）法一:平面與平面的距離到平面的距離．
中，，，，
由等體積可得，．
法二:
設平面的一個法向量為，
則，則可取，
，
平面與平面的距離為.
【變式8-3】（2023春·高二課時練習）如圖，在長方體中，，，求：
(1)點到直線BD的距離；
(2)點到平面的距離；
(3)異面直線之間的距離.
【解題思路】(1)建立空間直角坐標系，求直線的方向向量和向量的坐標，再求在上的投影向量的大小，結合勾股定理求點到直線BD的距離；(2)求平面的法向量，再求向量在向量上的投影的大小即可；(3)證明平面，利用向量方法求點到平面的距離即可.
【解題思路】（1）以點為原點，，，為，，軸的正方向建立空間直角坐標系，因為，，則，，，，，
所以，，所以在上的投影向量的大小為，又，所以點到直線BD的距離；
（2）由(1) ，，，
設平面的法向量，則，所以，
取，可得，，所以是平面的一個法向量，向量在法向量上的投影為，所以點到平面的距離為；
（3）由(1) ，，所以，所以，又平面，平面，所以平面，所以異面直線之間的距離與點到平面的距離相等，設平面的法向量，因為，則，所以，
取，可得，，所以是平面的一個法向量，向量在法向量上的投影為，所以點到平面的距離為；故異面直線之間的距離為.
【題型9 利用空間向量求空間角】
【例9】（2023春·湖北荊門·高二統考期末）如圖，三棱柱中，面面，，，．過的平面交線段于點（不與端點重合），交線段于點．

(1)求證：四邊形為平行四邊形；
(2)若，求直線與平面所成角的正弦值．
【解題思路】（1）利用線面平行的性質推導出，利用面面平行的性質可推導出，即可證得結論成立；
（2）證明出平面，然后以點為坐標原點，、所在直線分別為、軸，平面內過點且垂直于的直線為軸，建立空間直角坐標系，利用空間向量法可求得直線與平面所成角的正弦值.
【解題思路】（1）證明：在三棱柱中，，
因為平面，平面，所以，平面，
因為平面，平面，所以，，
因為平面平面，平面平面，平面平面，
所以，，因此，四邊形為平行四邊形．
（2）解：因為，平面平面，平面平面，
平面，所以，平面，
以點為坐標原點，、所在直線分別為、軸，
平面內過點且垂直于的直線為軸，建立如下圖所示的空間直角坐標系，

因，，
則，，，，
，，，，
，
設平面的法向量，則，
令，得，
而，設直線與平面所成角為，
于是得，
所以直線與平面所成角的正弦值為．
【變式9-1】（2023春·陜西西安·高一校考期末）如圖1，在中，，，，，都在上，且，，將，分別沿，折起，使得點，在點處重合，得到四棱錐，如圖2.

(1)求異面直線，所成角的余弦值；
(2)若為的中點，求鈍二面角的余弦值.
【解題思路】（1）（2）依題意可得，，建立空間直角坐標系，利用空間向量法計算可得.
【解題思路】（1）由題意可知，，，所以，
故，且，
∴，∴，∴，所以，
又，所以，即，，
故可以，，為，，軸建立空間直角坐標系如圖所示，

易知，，
則，，，，
∴，，
∴，
故異面直線，所成角的余弦值為；
（2）由（1）可知，
∴，，，
設平面法向量為，
由，則，令得，
設平面法向量為，
由，則，令得，
所以，
所以鈍二面角的余弦值為.
【變式9-2】（2023春·湖南衡陽·高二統考期末）如圖，在四棱錐中，四邊形是矩形，平面（垂足H在矩形內），E為棱的中點，平面.

(1)證明：；
(2)若，直線PC與平面所成角為，求平面與平面夾角的余弦值.
【解題思路】（1）延長交于點，連按，，由線面平行的性質得，進而確定H為CF的中點，利用三角形全等證結論；
（2）建立空間直角坐標系，求平面與平面的法向量，利用向量法求面面角的余弦值.
【解題思路】（1）延長交于點，連接，，
平面，面面，面，則，
又E為棱PC的中點，則H為CF的中點，
∴BH是直角三角形BCF斜邊上的中線，
∴，易知，則.
（2）以H為原點建立如圖所示的空間直角坐標系，

∵平面，∴CH是PC在平面內的射影，
∴是直線與面所成角，∴，
∴為等腰直角三角形，
設，則，則，∴，
∴，，，，，
∴，，，，
設平面的法向量為，
由，令，則.
設平面的法向量為，
由，令，則.
∴，平面與平面夾角的余弦值為.
【變式9-3】（2023春·江蘇連云港·高二統考期中）如圖，在四棱錐中，平面，與底面所成的角為45°，底面為直角梯形，，，．

(1)求直線與平面所成角的正弦值；
(2)求平面與平面所成的銳二面角的余弦值．
【解題思路】（1）以為坐標原點，建立的空間直角坐標系，求得向量，和平面的一個法向量，結合向量的夾角公式，即可求解；
（2）由平面的一個法向量，求得平面的一個法向量為，結合向量的夾角公式，即可求解．
【解題思路】（1）解：因為平面，且平面，所以，，
又因為，所以，
因為與底面所成的角為，所以，故，
以為坐標原點，，，所在直線分別為軸，軸，軸建立的空間直角坐標系，如圖所示，
因為，，可得，，，，
所以，，，
設平面的一個法向量為，可得，
取，則，可得，
所以，
所以直線與平面所成角的正弦值為．
（2）解：根據題意，平面的一個法向量，
設平面的一個法向量為，可得，
取，則，，所以
則，
所以平面與平面所成的銳二面角的余弦值為．
【題型10 利用空間向量研究存在性問題】
【例10】（2023·全國·高三對口高考）如圖所示的幾何體中，四邊形是等腰梯形，，，平面，，.

(1)求二面角的余弦值；
(2)在線段AB（含端點）上，是否存在一點P，使得平面.若存在，求出的值；若不存在，請說明理由.
【解題思路】（1）建立空間直角坐標系，利用法向量的夾角即可求解二面角，
（2）由平面法向量與直線方向向量垂直，結合向量共線，即可由坐標運算求解.
【解題思路】（1）過作于，由于，則,由于,且四邊形是等腰梯形，所以,在三角形中，由余弦定理可得，所以,故,

以為坐標原點，，為軸，軸，過點作的平行線為軸，建立空間直角坐標系，設，則，
設面的法向量，
則，即，取，得．
設面的法向量，
則，即，則取，得．
，
由幾何體的特征可知二面角的平面角為銳角，
二面角的余弦值為．
（2），,， 面，
面．
設,
若平面，則 ,所以，
所以.
【變式10-1】（2023·湖北襄陽·校考模擬預測）在三棱錐P-ABC中，若已知，，點P在底面ABC的射影為點H，則
(1)證明：
(2)設，則在線段PC上是否存在一點M，使得與平面所成角的余弦值為，若存在，設，求出的值，若不存在，請說明理由.
【解題思路】（1）由條件證明，再證明，由此可得，由線面垂直判定定理證明平面，由此證明；
（2）建立空間直角坐標系，技術存在點滿足條件，由條件求平面的法向量和直線的方向向量，由條件列方程求即可.
【解題思路】（1）因為點P在底面ABC的射影為點H，
所以平面，又平面，
所以，
因為，，，平面，
所以平面，又平面，
所以，
因為，，，平面，
所以平面，又平面，
所以，
因為，，
所以點為的垂心，所以，
因為，，平面，，
所以平面，又平面，
所以；
（2）延長交于點，由（1）可得，
又，所以點為線段的中點，
所以，同理可得，
所以為等邊三角形，又，所以，
如圖，以點為原點，以為軸的正方向，建立空間直角坐標系，
則，
故，
設存在點M，使得BM與平面所成角的余弦值為，且，
則，
設平面的法向量為，，
則，所以，
令，可得，
所以為平面的一個法向量，
所以，
設直線BM與平面所成角為，則，又，
所以，故，
所以或，又，
所以.
所以在線段PC上存在點M，使得BM與平面PAB所成角的余弦值為，且.
【變式10-2】（2023·河北衡水·河北校考三模）圖1是直角梯形ABCD，，∠D＝90°，四邊形ABCE是邊長為2的菱形，并且∠BCE＝60°，以BE為折痕將△BCE折起，使點C到達的位置，且．
(1)求證：平面平面ABED．
(2)在棱上是否存在點P，使得點P到平面的距離為？若存在，求出直線EP與平面所成角的正弦值；若不存在，請說明理由．
【解題思路】（1）在圖1中，連接，交于O，由幾何關系可得，，結合圖2易得 是二面角 的平面角，由勾股定理逆定理可證，進而得證；
（2）以，， 為 x，y，z 軸建立空間直角坐標系，設 ，，求得，同時求出平面的法向量，由點面距離的向量公式求得，進而求得，結合向量公式可求直線EP與平面所成角的正弦值.
【解題思路】（1）如圖所示：
在圖1中，連接，交于O，因為四邊形是邊長為2的菱形，并且，所以，且．
在圖 2 中， 相交直線 ，均與 垂直， 所以 是二面角 的平面角， 因為 ， 所以 ，，所以平面 平面 ；
（2）由 （1） 知， 分別以，， 為 x，y，z 軸建立如圖 2 所示的空間直角坐標系， 則 ，，，，， ，，，，.
設 ，，
則 .
設平面 的法向量為 ，
則， 即 ， 取 ，
因為點 到平面 的距離為 ，
所以 ， 解得 ，
則 ， 所以 .
設直線 與平面 所成的角為 ，
所以直線 與平面 所成角的正弦值為 .
【變式10-3】（2023春·廣東佛山·高二校考階段練習）如圖，在四棱錐中，已知底面是正方形，底面，且，是棱上動點.
(1)證明：平面.
(2)線段上是否存在點，使二面角的余弦值是？若存在，求的值；若不存在，請說明理由.
【解題思路】（1）利用正方形性質、線面垂直的性質和線面垂直的判定定理進行證明即可；
（2）以為坐標原點建立空間直角坐標系，設，利用向量線性運算可得，根據二面角的向量求法可構造方程求得的值.
【解題思路】（1）連接，交于點，
四邊形為正方形，；
平面，平面，，
又，平面，平面.
（2）以為坐標原點，正方向為軸，可建立如圖所示空間直角坐標系，
則，，，，，
，，，，
假設在線段上存在點，使得二面角的余弦值為，
設，則，，
設平面的法向量，
則，令，解得：，，；
由（1）知：平面，平面的一個法向量為；
，解得：，
當，即時，二面角的余弦值為.

展開更多......

收起↑