資源簡介

第四章 數列
第4.1.1講 數列的概念與表示
1.通過日常生活和數學中的實例了解數列的概念和表示方法(列表法、圖象法、通項公式法).　
2.了解數列是一種特殊的函數.　
3.能根據數列的前幾項寫出數列的通項公式，并能利用數列的通項公式寫出數列的任意項.
1、數列的概念與分類
2、由數列的前幾項求通項公式
3、數列通項公式的簡單應用
知識點一　數列的概念
1.數列的概念
（1）按照確定的順序排列的一列數稱為數列，數列中的每一個數叫做這個數列的項.數列的第n個個位置上的數叫做這個數列的第n項，其中第1項也叫做首項.
（2）數列的一般形式是a1，a2，…，an，…，簡記為{an}，這里n是序號.
2.函數與數列的關系
數列{an}是從正整數集N*(或它的有限子集{1，2，…，n})到實數集R的函數，其自變量是序號，對應的函數值是數列的第n項an，記為an＝f(n).
知識點二　數列的分類
1.按項數分類：項數有限的數列叫有窮數列；項數無限的數列叫無窮數列.
2.按項的變化趨勢分類
類別 含義
遞增數列 從第2項起，每一項都大于它的前一項的數列
遞減數列 從第2項起，每一項都小于_它的前一項的數列
常數列 各項都相等的數列
知識點三　數列的通項公式
1.如果數列{an}的第n項an與它的_11序號n之間的對應關系可以用一個式子來表示，那么這個式子叫做這個數列的通項公式.
2.數列是特殊的函數，還常用__12列表法和13圖象法表示數列.用圖象法表示數列時，其圖象是一些離散的點.
題型1、數列的概念與分類
1．數列的通項公式是，，則它的圖象是（ ）
A．直線 B．直線上孤立的點
C．拋物線 D．拋物線上孤立的點
2．已知，則數列是（ ）
A．遞增數列 B．遞減數列
C．常數列 D．不確定
3．下列結論中，正確的是（ ）
A．數列可以看作是一個定義在正整數集（或它的有限子集）上的函數
B．數列的項數一定是無限的
C．數列的通項公式的形式是唯一的
D．數列1，3，2，6，3，9，4，12，5，15，…不存在通項公式
4．下列數列中，既是遞增數列又是無窮數列的是（ ）
A．1，，，，… B．，，，
C．，，，，… D．1，，，…，
5．下列說法正確的是（ ）
A．數列與是相同的
B．數列可以表示為
C．數列與是相同的數列
D．數列的第項為
題型2、由數列的前幾項求通項公式
6．在數列1，2，，，，中，是這個數列的（ ）
A．第16項 B．第24項 C．第26項 D．第28項
7．下面圖形由小正方形組成，請觀察圖①至圖④的規律，并依此規律，寫出第n個圖形中小正方形的個數是（ ）

A． B． C． D．
8．已知數列滿足，且，則（ ）
A． B． C． D．
9．若，則（ ）
A．55 B．56 C．45 D．46
10．已知數列的項滿足，而，則＝（ ）
A． B． C． D．
題型3、數列通項公式的簡單應用
11．下列敘述正確的是（ ）
A．數列是遞增數列
B．數列0，1，2，3，…的一個通項公式為
C．數列0，0，0，1，…是常數列
D．數列2，4，6，8與數列8，6，4，2是相同的數列
12．在數列中，若，則的值為（ ）
A．17 B．23 C．25 D．41
13．數列1，，，…的通項公式可能是（ ）
A． B． C． D．
14．已知數列的通項公式，記，通過計算，歸納出的表達式是（ ）
A． B． C． D．
15．已知數列滿足，，則（ ）
A．2023 B．2024 C．4045 D．4047
一、單選題
16．數列的通項公式可能是（ ）
A． B． C． D．
17．數列的通項公式是，，則它的圖象是（ ）
A．直線 B．直線上孤立的點
C．拋物線 D．拋物線上孤立的點
18．數列的通項公式為（ ）
A．
B．
C．
D．
19．已知數列滿足：，則等于（ ）
A．32 B．64 C．48 D．128
20．在數列中，，（），則的前2022項和為（ ）
A．589 B．590 C． D．
21．下列數列是遞減數列的是（ ）
A． B．
C． D．
22．已知數列的通項公式為，則數列中的最大項的項數為（ ）
A．2 B．3 C．2或3 D．4
23．已知滿足對一切正整數均有且恒成立，則實數的范圍是（ ）
A． B． C． D．
二、多選題
24．（多選題）下列說法不正確的是（ ）
A．數列可以表示為
B．數列與數列是相同的數列
C．數列的第項為1＋
D．數列可記為
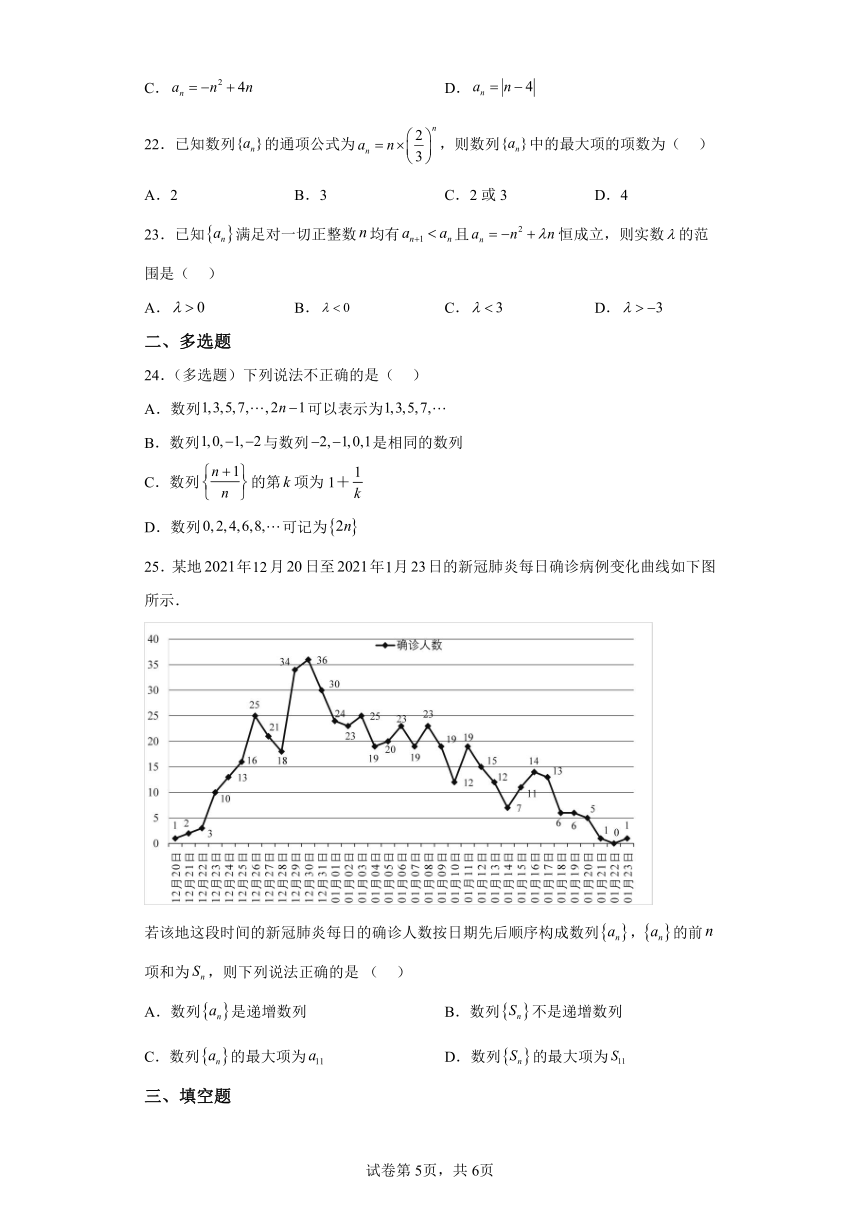
25．某地年月日至年月日的新冠肺炎每日確診病例變化曲線如下圖所示．
若該地這段時間的新冠肺炎每日的確診人數按日期先后順序構成數列，的前項和為，則下列說法正確的是（ ）
A．數列是遞增數列 B．數列不是遞增數列
C．數列的最大項為 D．數列的最大項為
三、填空題
26．數列 的一個通項公式為 .
27．對于等差數列和等比數列，我國古代很早就有研究成果，北宋大科學家沈括在《夢溪筆談》中首創的“隙積術”，就是關于高階等差級數求和的問題.現有一貨物堆，從上向下查，第一層有2個貨物，第二層比第一層多3個，第三層比第二層多4個，第四層比第三層多5個，以此類推，則第20層貨物的個數為 .
四、問答題
28．求下列數列的一個通項公式：
(1)，2，，4，…
(2)，，，，…
29．一個正方形被等分成九個相等的小正方形，將最中間的一個正方形挖掉，得圖①；再將剩下的每個正方形都分成九個相等的小正方形，并將其最中間的一個正方形挖掉，得圖②；如此繼續下去……

(1)圖③中共挖掉了多少個正方形？
(2)求每次挖掉的正方形個數所構成的數列的一個遞推公式．
30．已知數列的通項公式是，畫出該數列的圖象．并根據圖象，判斷從第幾項起，這個數列是遞增的．
試卷第1頁，共3頁
試卷第1頁，共3頁
參考答案：
1．B
【分析】根據數列的知識確定正確答案.
【詳解】數列對應點為，
所以圖象是直線上孤立的點.
故選：B
2．A
【分析】
根據遞增數列的定義即可判斷出答案.
【詳解】由題意可知，
即從第二項起數列的每一項比它的前一項大，所以數列是遞增數列；
故選：A
3．A
【分析】
利用數列的定義判斷A；舉例說明判斷BC；寫出數列通項公式判斷D作答.
【詳解】對于A，由數列定義知，A正確；
對于B，數列只有5項，該數列項數有限，B錯誤；
對于C，數列的通項公式可以為，
也可以為，該數列通項公式不唯一，C錯誤；
對于D，該數列的通項公式可以為，D錯誤.
故選：A
4．C
【分析】由無窮數列的概念，數列的單調性利用排除法判斷．
【詳解】A，B都是遞減數列，D是有窮數列，只有C符合題意．
故選：C．
5．D
【分析】
運用數列的定義、數列及項的表示方法、由通項寫出數列的項可判斷各個選項.
【詳解】對于A項，數列與是不同的，表示數列，而表示數列中的第項，故A項錯誤；
對于B項，是一個集合，故B項錯誤；
對于C項，兩個數列中的數雖然相同，但順序不同，不是相同的數列，故C項錯誤；
對于D項，，故D項正確.
故選：D.
6．B
【分析】根據題意求出數列的通項公式，結合通項公式分析求解.
【詳解】數列可化為 ，
所以，
令，解得，
所以是這個數列的第項，
故選：B．
7．C
【分析】
由，，，可推測，以上式子累加，結合等差數列的求和公式可得答案．
【詳解】
，，，，，，，，
等式兩邊同時累加得，即，也符合該式，
所以第個圖形中小正方形的個數是．
故選：C
8．B
【分析】
根據題意，兩邊取倒數，然后累加即可得到結果.
【詳解】，則，，，…，，以上各式相加可得，，.
故選：B
9．D
【分析】在數列遞推式中依次取，得到個等式，累加后求出數列的通項公式，即可求出答案.
【詳解】由，
得，，
，，，
累加得，
，
當時，上式成立，
則，
所以.
故選：D
10．B
【分析】
由，可得，然后利用累乘法可求得結果
【詳解】由，得，
所以，，，……，，，（），
所以，
所以，
因為，所以，
因為滿足上式，所以，
故選：B
11．A
【分析】作差即可判斷A項；代入檢驗，即可判斷B項；根據常數列以及數列的概念，即可判斷C、D.
【詳解】對于A項，設，
則對恒成立，
所以，數列是遞增數列.故A正確；
對于B項，當時，與第一項為0不符.故B項錯誤；
對于C項，數列中的項并不完全相同.故C項錯誤；
對于D項，根據數列的概念，數列與順序有關.
所以，數列2，4，6，8與數列8，6，4，2不是相同的數列.故D項錯誤.
故選：A.
12．A
【分析】根據給定的通項公式，直接計算即可.
【詳解】依題意，.
故選：A
13．A
【分析】代入即可結合選項逐一排除.
【詳解】當時，對于B中，
當時，對于C中，對于D中，
四個選項中只有同時滿足，，.
故選：A
14．C
【分析】求出的值，歸納它們的值與序號的關系，即可得答案.
【詳解】由題意數列的通項公式，
則，，
，
可看出分子上的值為相應項的序號加2，分母為相應序號加1后的2倍，
故歸納出的表達式是，
故選：C
15．C
【分析】根據遞推關系化簡后，由累乘法直接求.
【詳解】，
，
即，
可得，
.
故選：C.
16．D
【分析】由具體數列判斷通項公式問題，最簡單的方法即是賦值代入檢驗判斷即可.
【詳解】對于選項A，當時，，故A項錯誤；
對于B選項，當時，，故B項錯誤；
對于C選項，當時，，故C項錯誤；
對于D項，因數列可以寫成 ，故其通項公式可以寫成，故D項正確.
故選：D.
17．B
【分析】根據數列的知識確定正確答案.
【詳解】數列對應點為，
所以圖象是直線上孤立的點.
故選：B
18．C
【分析】根據規律求得數列的一個通項公式，從而確定正確答案.
【詳解】數列，
即，
所以數列的通項公式可以為.
故選：C
19．B
【分析】由數列的通項直接計算得出答案.
【詳解】由，令，得，
故選：B.
20．C
【分析】
通過遞推式計算出前幾項，找到數列的周期，利用周期性求解即可.
【詳解】
因為，（），所以，，
，，而，所以數列是以4為周期的周期數列，
所以的前2022項和.
故選：C
21．B
【分析】利用函數方法依次判斷每個選項數列的增減性得到答案.
【詳解】對選項A：為遞增數列；
對選項B：為遞減數列；
對選項C：，先增后減數列；
對選項D：，先減后增數列.
故選：B.
22．C
【分析】
利用差比較法確定正確答案.
【詳解】；；，，
當時，，所以，
所以數列中的最大項的項數或.
故選：C
23．C
【分析】根據題意整理可得對一切正整數恒成立，根據恒成立問題分析求解.
【詳解】因為滿足對一切正整數均有且恒成立，
即恒成立，化為，
可知對一切正整數恒成立，所以，
故選：C.
24．ABD
【分析】根據數列的概念求得正確答案.
【詳解】A選項，數列和數列，
前者是有限項，后者是無限項，所以兩個數列不一樣，A選項錯誤.
B選項，數列與數列的項的順序不相同，
所以不是相同數列，B選項錯誤.
C選項，，所以數列的第項為1＋，C選項正確.
D選項，數列可記為，所以D選項錯誤.
故選：ABD
25．BC
【分析】由每日確診病例變化曲線可判斷每日病例的增減情況，可知的項的變化情況，判斷A，C；由變化曲線可知月日沒有確診病例，可知，判斷B；根據病例的增加情況判斷D.
【詳解】解：由每日確診病例變化曲線圖可知：數列一開始是先遞增到，再遞減至，
即數列不是遞增數列，故A選項錯誤，
因為年月日沒有確診病例，所以，數列不是遞增數列，B選項正確．
由每日確診病例變化曲線圖可知：數列的最大項是第項，即是最大項，故C選項正確．
由每日確診病例變化曲線圖可知：第天以后，每天還是有確診病例，故數列的最大項不是．
故選：BC．
26．
【分析】觀察其分子，分母與項之間的關系即可求.
【詳解】可化為，
所以分子部分為，
分母部分為，
奇數項為正，偶數項為負，則，
則.
故答案為：
27．230
【分析】由題意可得，，利用累加法即可求.
【詳解】解：由題意可知，，，，，累加可得.
故答案為：230
28．(1)
(2)
【分析】直接依據所給數列的項的特征和項與項之間的規律求解即可．
【詳解】（1）1，2，3，4，…，的一個通項為，所以，2，，4，…的一個通項為
（2）1，4，9，16，…，可用表示，
而2，5，10，17，…可用，故
29．(1)73
(2)
【分析】（1）觀察圖中每次挖掉的正方形個數，是前一次挖掉的個數乘以8，再加上前兩次挖的個數可得總數；
（2）觀察圖形可得規律，每次挖掉的正方形個數是前一次的8倍，由此可得遞推公式.
【詳解】（1）因為第一次挖掉1個正方形，第二次挖掉8個，第三次挖掉 個，
所以圖③中共挖掉 個正方形.
（2）由（1）知，第一次挖 個正方形，第二次挖掉 個，第三次挖掉 個，
以此類推，第n次挖掉，故 ，
則遞推公式為 .
30．見解析
【分析】利用描點法畫圖，結合圖象分析單調性即可.
【詳解】列表如下：
1 2 3 4 5 6 7 8 ……
-30 -30 -28 -24 -18 -10 0 12 ……
作圖如下：

如圖所示，易知數列首項與第二項相同，從第二項開始每一項都大于前一項，即從第二項開始遞增.
答案第1頁，共2頁
答案第1頁，共2頁

展開更多......

收起↑