資源簡介

1.7.2 正切函數的圖象與性質
【學習目標】
1.掌握正切函數的周期性和奇偶性.(數學抽象)
2.掌握正切函數的性質.(數學運算)
【自主預習】
1.正切函數與正弦、余弦函數的關系是什么
2.正切函數的定義域是什么
3.正切函數在定義域上是單調函數嗎
4.正切曲線是中心對稱圖形嗎 若是，其對稱中心是什么 其是軸對稱圖形嗎
5.正切函數y=tan x的圖象與直線x=kπ+，k∈Z有公共點嗎
1.判斷下列結論是否正確.(正確的打“√”，錯誤的打“×”)
(1)正切函數的定義域和值域都是R. (　　)
(2)正切函數在R上是單調遞增的. (　　)
(3)正切曲線是中心對稱圖形，有無數個對稱中心. (　　)
(4)正切函數的最小正周期為π. (　　)
2.函數y=tanx+的定義域為　　　　　　　.
3.函數y=tan x，x∈-，的最大值為　　　　.
4.函數y=tanx-的單調遞增區間是　　　　.
【合作探究】
　正切函數的圖象
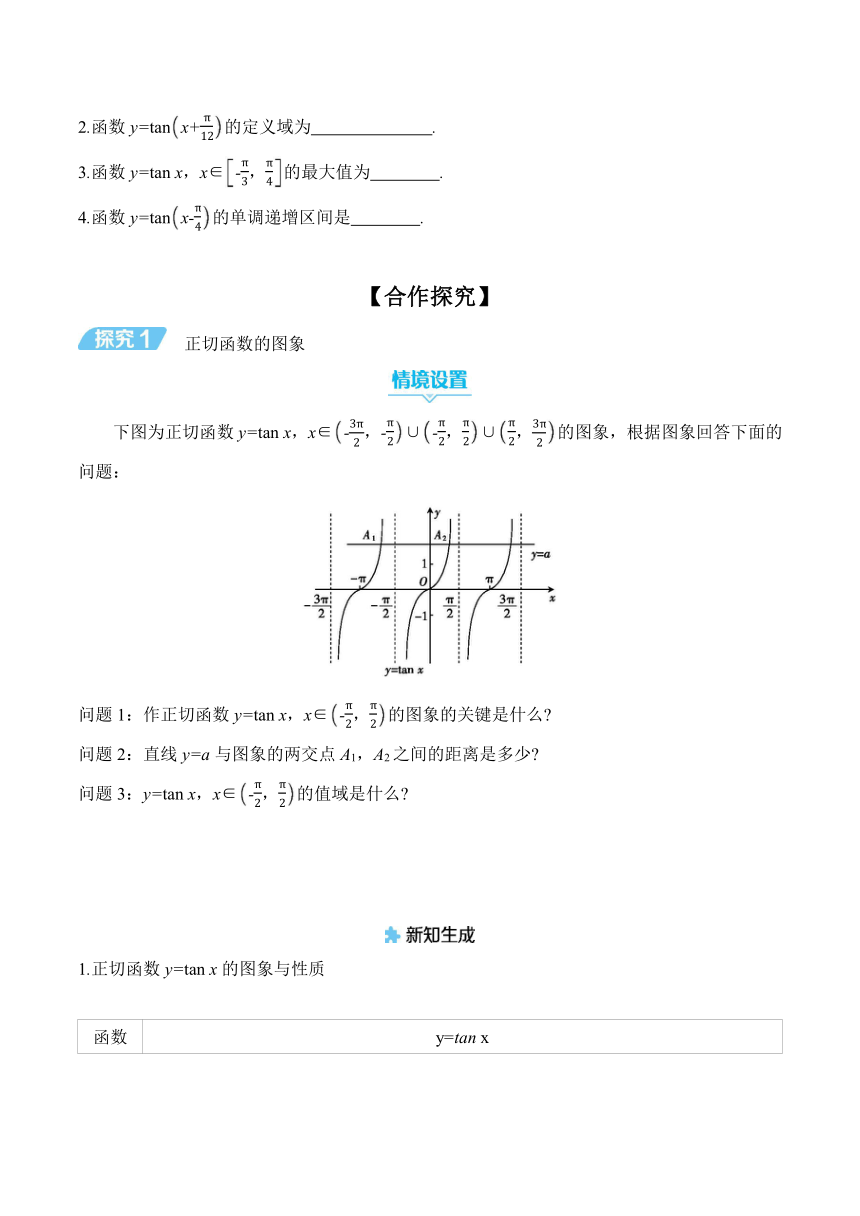
　　下圖為正切函數y=tan x，x∈-，-∪-，∪，的圖象，根據圖象回答下面的問題：
問題1：作正切函數y=tan x，x∈-，的圖象的關鍵是什么
問題2：直線y=a與圖象的兩交點A1，A2之間的距離是多少
問題3：y=tan x，x∈-，的值域是什么
1.正切函數y=tan x的圖象與性質
函數 y=tan x
圖象
定義域
值域
周期 最小正周期為
奇偶性
2.(1)正切函數的圖象是由被相互平行的直線x=kπ+，k∈Z隔開的無窮多支曲線組成的.
(2)正切函數y=tan x，x∈-，的簡圖可由“三點兩線法”確定.
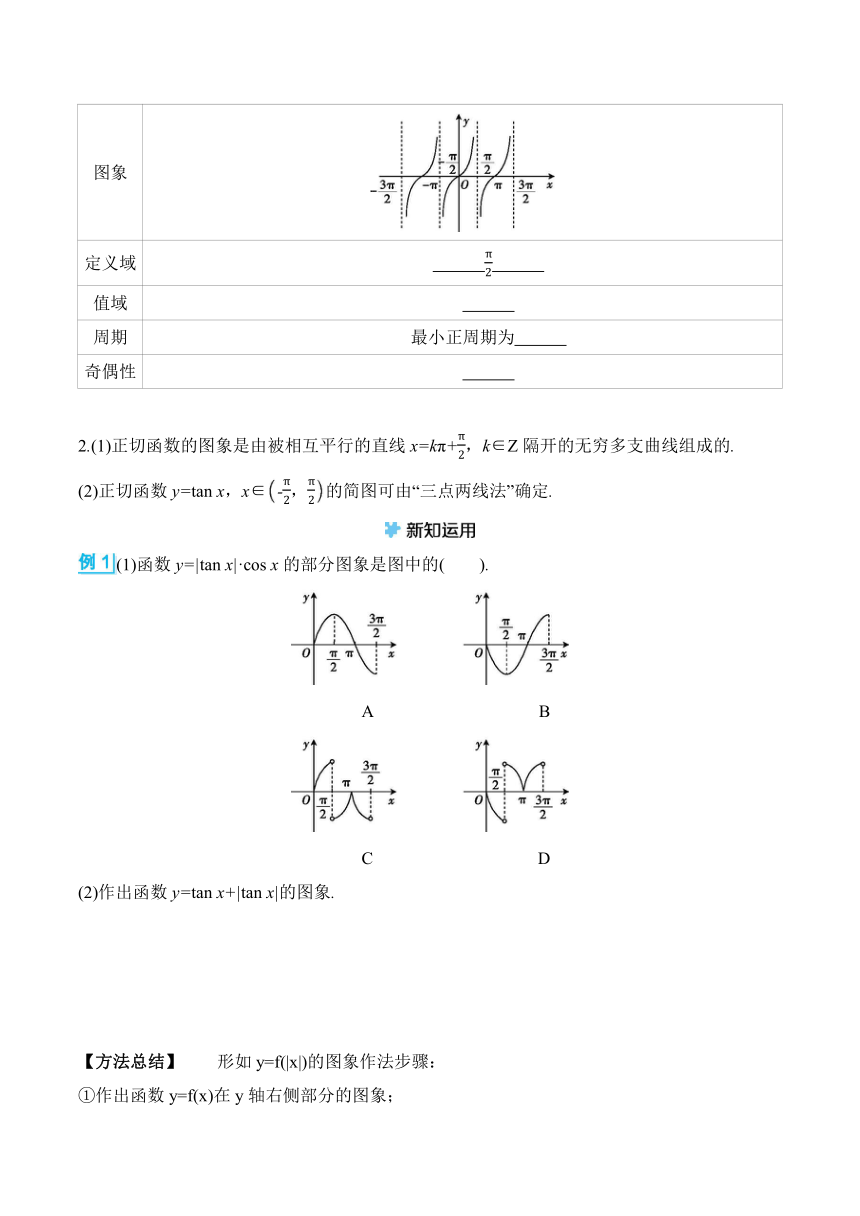
(1)函數y=|tan x|·cos x的部分圖象是圖中的(　　).
　　　A　　　 　　　　　　B
　　　C　　 　　　　　　　D
(2)作出函數y=tan x+|tan x|的圖象.
【方法總結】　　形如y=f(|x|)的圖象作法步驟：
①作出函數y=f(x)在y軸右側部分的圖象；
②函數y=f(|x|)為偶函數，故將y軸右側的圖象對稱到y軸左側，保留y軸右側部分，即可得到函數y=f(|x|)的圖象.
已知函數f(x)=.
(1)求函數f(x)的定義域；
(2)用定義判斷函數f(x)的奇偶性；
(3)作出函數f(x)在[-π，π]上的圖象.
　正切函數圖象的應用
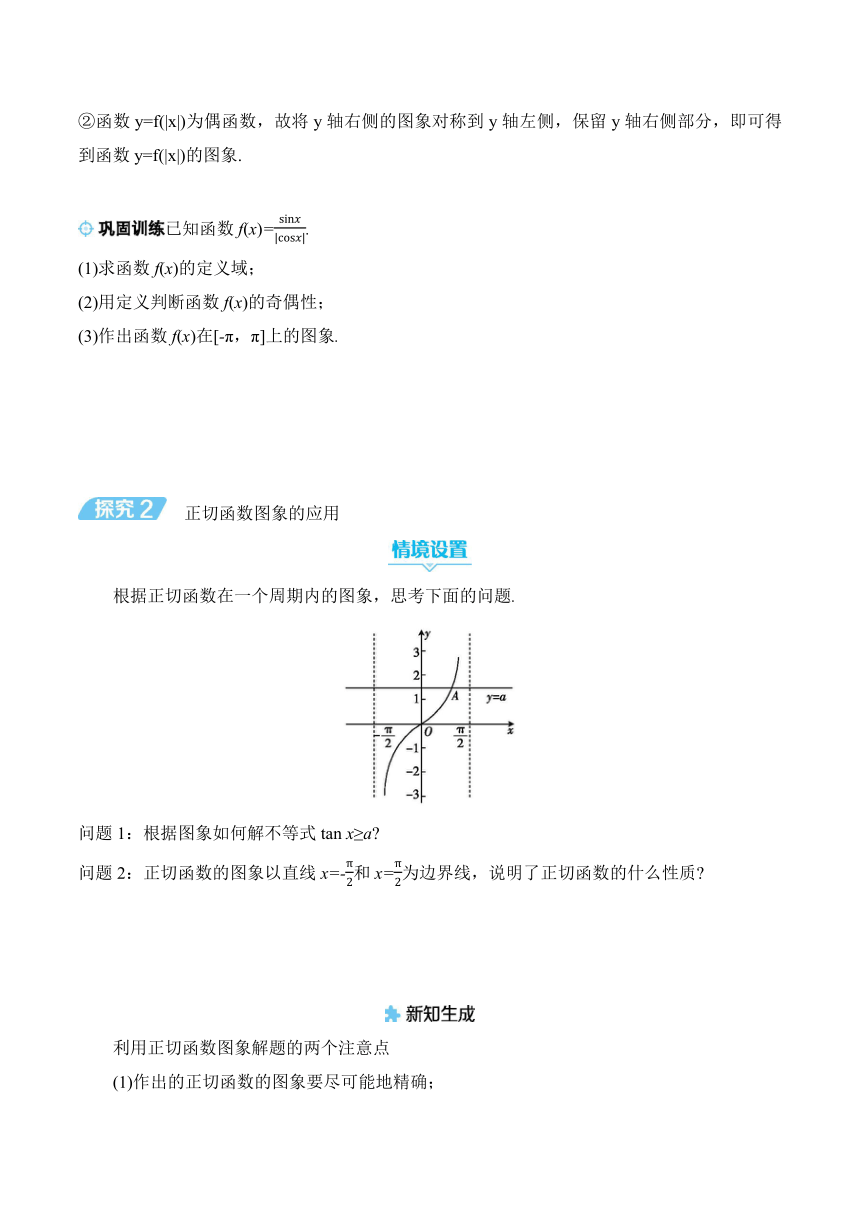
　　根據正切函數在一個周期內的圖象，思考下面的問題.
問題1：根據圖象如何解不等式tan x≥a
問題2：正切函數的圖象以直線x=-和x=為邊界線，說明了正切函數的什么性質
利用正切函數圖象解題的兩個注意點
(1)作出的正切函數的圖象要盡可能地精確；
(2)解題時一般先利用一個周期內的圖象，再轉化到整個定義域內.
函數y=的定義域為　　　　，值域為　　　　.
【方法總結】　　求與正切函數有關的函數的定義域時，除了要滿足求函數定義域的一般要求外，還要保證正切函數y=tan x有意義，即x≠kπ+，k∈Z.而對于構建的三角不等式，常利用三角函數的圖象求解.
求函數y=ln(tan x)的定義域.
　正切函數的性質及其應用
　　對于正切函數的圖象，數學老師請同學們類比正弦函數和余弦函數的性質，描述正切函數的單調性、奇偶性、周期性，其結果如下.
王浩宇說：“函數y=tan x在定義域R內單調遞增.”
李琦說：“函數y=tan x的圖象的對稱中心為(kπ，0)，k∈Z.”
張瑜說：“y=Atan(2x+φ)(A>0，ω>0)的最小正周期是2π.”
問題：上面同學的說法哪些是錯誤的 請說明理由.
y=Atan(ωx+φ)(ω≠0)的性質
(1)單調性：只有一種單調區間，由-+kπ<ωx+φ<+kπ，k∈Z確定.
①當Aω>0時，所得的區間為單調遞增區間；
②當Aω<0時，所得的區間為單調遞減區間.
(2)周期性：T=.
(3)對稱性：圖象的對稱中心為，0，k∈Z，不具有軸對稱性.
(4)奇偶性：當φ=，k∈Z時為奇函數，否則不具有奇偶性.
(1)比較下列兩個數的大小(用“>”或“<”填空)：
①tan　　　　tan；
②tan　　　　tan-.
(2)求函數y=tanx+的單調遞增區間.
【方法總結】　　(1)運用正切函數的單調性比較大小的方法
①運用函數的周期性或誘導公式將角化到同一單調區間內.
②運用單調性比較大小關系.
(2)求函數y=tan(ωx+φ)的單調區間的方法
y=tan(ωx+φ)(ω>0)的單調區間的求法是把ωx+φ看成一個整體，解-+kπ<ωx+φ<+kπ，k∈Z即可.當ω<0時，先用誘導公式把ω化為正值再求單調區間.
函數f(x)=tan-+的單調區間為　　　　.
已知函數f(x)=Atan(ωx+φ)ω>0，|φ|<的部分圖象如圖所示，則f=　　　　.
比較tan與tan的大小.
【隨堂檢測】
1.函數y=2tan3x+的最小正周期是(　　).
A. B.
C. D.
2.函數f(x)=tanx+的單調遞增區間為(　　).
A.kπ-，kπ+，k∈Z
B.(kπ，(k+1)π)，k∈Z
C.kπ-，kπ+，k∈Z
D.kπ-，kπ+，k∈Z
3.求函數y=tanx-的定義域、最小正周期及單調區間.
參考答案
1.7.2 正切函數的圖象與性質
自主預習·悟新知
預學憶思
1.tan x=(cos x≠0).
2.xx≠kπ+，k∈Z.
3.不是.
4.正切曲線是中心對稱圖形，對稱中心為，0(k∈Z)，不是軸對稱圖形.
5.沒有.正切曲線是由被互相平行的直線x=kπ+(k∈Z)隔開的無窮多支曲線組成的.
自學檢測
1.(1)×　(2)×　(3)√　(4)√
2.　【解析】令x+≠kπ+(k∈Z)，解得x≠kπ+(k∈Z)，故函數的定義域為.
3.1　【解析】正切函數在-，上單調遞增，故函數的最大值為tan=1.
4.-+kπ，+kπ，k∈Z　【解析】令kπ-合作探究·提素養
探究1　情境設置
問題1：點-，-1，(0，0)，，1及兩條漸近線x=-和x=在作圖中起著關鍵的作用.
問題2：由圖象結合正切函數的周期性可知，兩交點之間的距離為π.
問題3：R.
新知生成
1.x∈Rx≠kπ+，k∈Z　R　π　奇函數
新知運用
例1　(1)C　【解析】(1)因為y=|tan x|·cos x=·cos x=
所以由正弦函數的圖象與性質可得，函數y=|tan x|·cos x的部分圖象是C.
(2)y=tan x+|tan x|=其圖象如圖所示.
鞏固訓練　【解析】(1)由cos x≠0，得x≠kπ+，k∈Z，
所以函數f(x)的定義域是.
(2)由(1)知函數f(x)的定義域關于原點對稱，
因為f(-x)===-f(x)，
所以f(x)是奇函數.
(3)因為f(x)=
所以f(x)在[-π，π]上的圖象如圖所示.
探究2　情境設置
問題1：在同一坐標系內作出正切函數y=tan x，x∈-，和y=a的圖象，如上圖，記其交點為A，橫坐標記為x1，則不等式tan x≥a的解集為xx1+kπ≤x<+kπ，k∈Z.
問題2：由圖象可知，正切函數的圖象向下、向上無限延伸，且無限接近直線x=-和x=，但永遠不會相交，因此，y=tan x中，x≠+kπ，k∈Z.
新知運用
例2　xkπ+≤x【解析】由tan x≥知，kπ+≤x鞏固訓練　【解析】由題意得
即
故定義域為kπ，kπ+，k∈Z.
探究3　情境設置
問題：王浩宇的說法錯誤，因為<，但tan不小于tan.正切函數y=tan x在它的任一個連續區間kπ-，kπ+，k∈Z內單調遞增；
李琦的說法錯誤，，0也是正切函數y=tan x的圖象的一個對稱中心；
張瑜的說法錯誤，因為y=Atan(2x+φ)的最小正周期是.
新知運用
例3　(1)①<　②<　【解析】(1)①tan=tan，且0<<<，又y=tan x在0，上單調遞增，
所以tan②tan=tan，tan-=tan，因為0<<<，且y=tan x在0，上單調遞增，
所以tan(2)由-+kπ所以函數y=tanx+的單調遞增區間為-+2kπ，+2kπ(k∈Z).
鞏固訓練1　2kπ-，2kπ+，k∈Z　【解析】f(x)=tan-+=-tan-.由kπ-<-所以函數f(x)=tan-+的單調遞減區間是2kπ-，2kπ+，k∈Z.
鞏固訓練2　　【解析】由圖可知T=，故ω=2，函數圖象的一個對稱中心為-，0，因此tan-+φ=0，又|φ|<，所以φ=，所以f(0)=Atan=1，所以A=1，得f(x)=tan2x+，所以f=tan2×+=tan=.
鞏固訓練3　【解析】因為tan=tan，tan=tan，又0<<<，y=tan x在0，上單調遞增，所以tan隨堂檢測·精評價
1.B　【解析】T==.
2.C　【解析】因為kπ-所以f(x)的單調遞增區間為kπ-，kπ+，k∈Z.
3.【解析】由x-≠+kπ，k∈Z，
得x≠+2kπ，k∈Z，
所以函數y=tanx-的定義域為xx≠+2kπ，k∈Z.
因為T==2π，
所以函數y=tanx-的最小正周期為2π.
由-+kπ得-+2kπ所以函數y=tanx-的單調遞增區間為-+2kπ，+2kπ，k∈Z，無單調遞減區間.

展開更多......

收起↑