 資源預覽
資源預覽


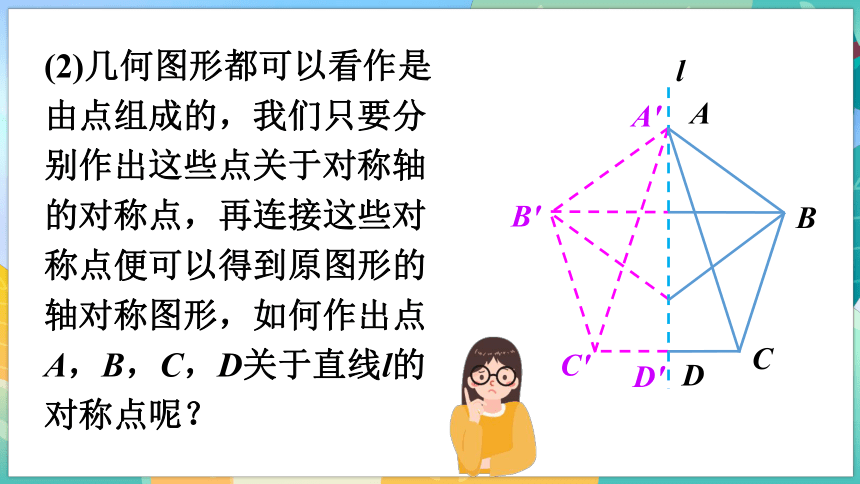



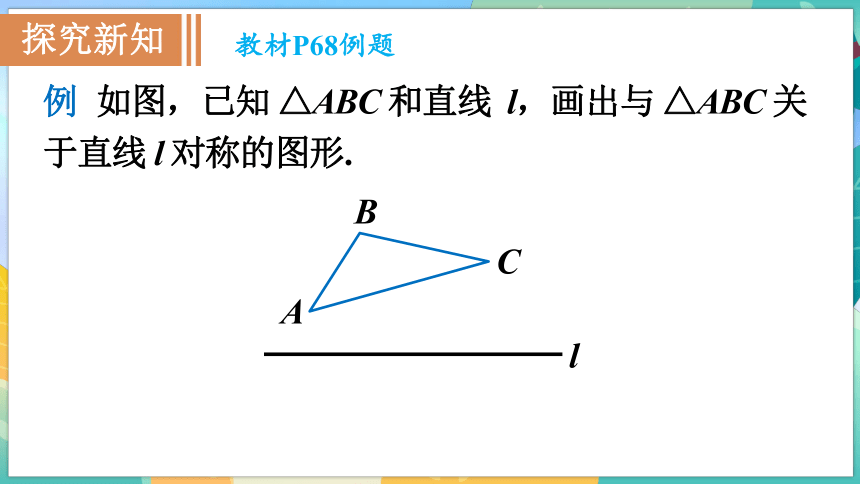
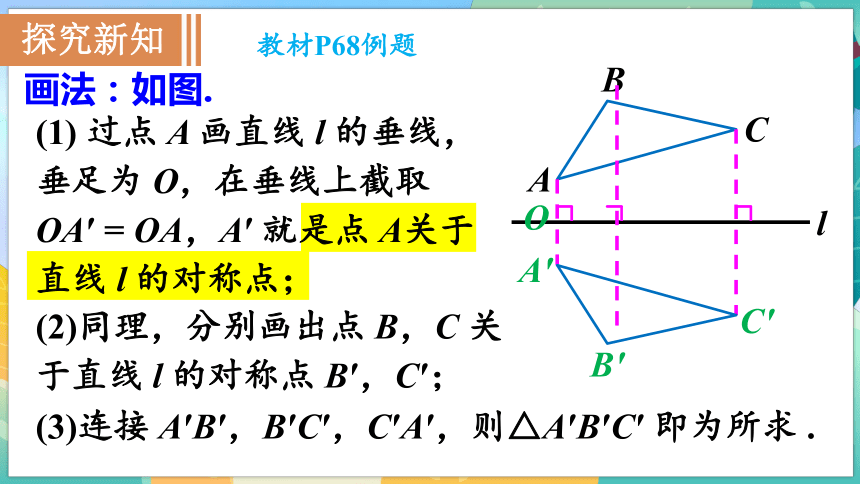
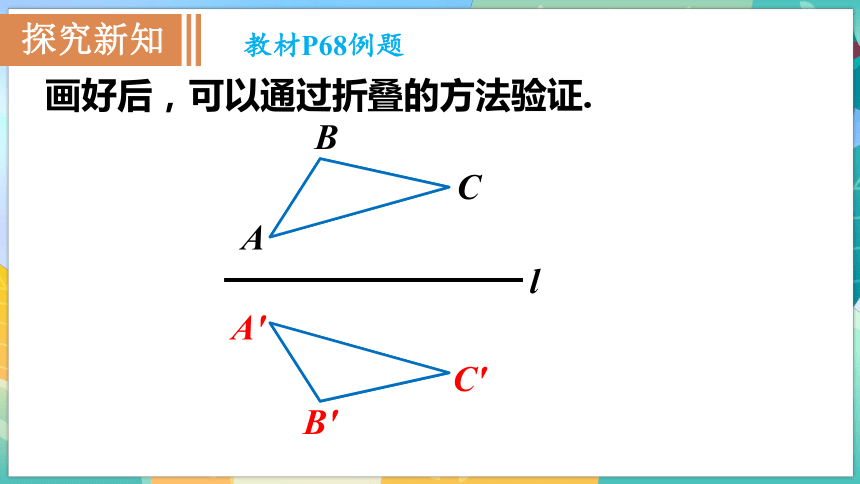
 資源預覽
資源預覽








