資源簡介

(共17張PPT)
新授課
6.5 正態(tài)分布
前面討論了離散型隨機變量，它們的取值是可以一一列舉的.但在實際問題中，還有許多隨機變量可以取某一區(qū)間中的所有值.例如：
1.某一自動裝置無故障運轉(zhuǎn)的時間X是一個隨機變量，它可以取區(qū)間
(0，+∞)內(nèi)的所有值.
2.某種產(chǎn)品的壽命(使用時間)X是一個隨機變量，它可以取區(qū)間[0,b]或[0，+∞)內(nèi)的所有值.
怎樣描述這樣的隨機變量的分布情況呢？
1.利用實際問題的頻率分布直方圖，了解正態(tài)分布曲線的特點及曲線所表示的意義.
2.了解正態(tài)分布的均值、方差及3σ原則，會用正態(tài)分布去解決實際問題.
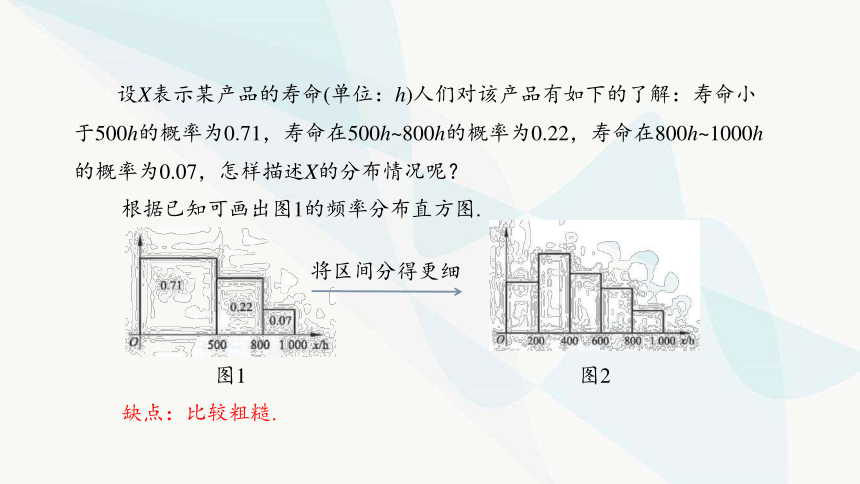
設(shè)X表示某產(chǎn)品的壽命(單位：h)人們對該產(chǎn)品有如下的了解：壽命小于500h的概率為0.71，壽命在500h~800h的概率為0.22，壽命在800h~1000h的概率為0.07，怎樣描述X的分布情況呢？
根據(jù)已知可畫出圖1的頻率分布直方圖.
圖1
缺點：比較粗糙.
將區(qū)間分得更細(xì)
圖2
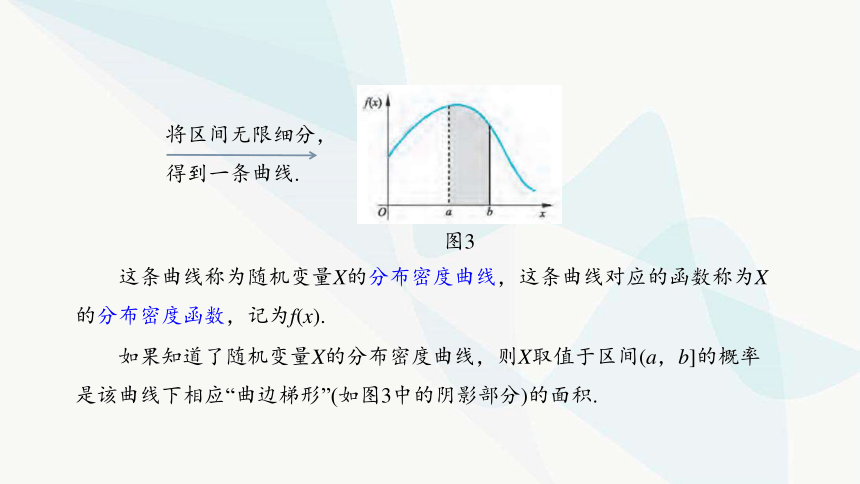
將區(qū)間無限細(xì)分，
得到一條曲線.
圖3
這條曲線稱為隨機變量X的分布密度曲線，這條曲線對應(yīng)的函數(shù)稱為X的分布密度函數(shù)，記為f(x).
如果知道了隨機變量X的分布密度曲線，則X取值于區(qū)間(a，b]的概率是該曲線下相應(yīng)“曲邊梯形”(如圖3中的陰影部分)的面積.
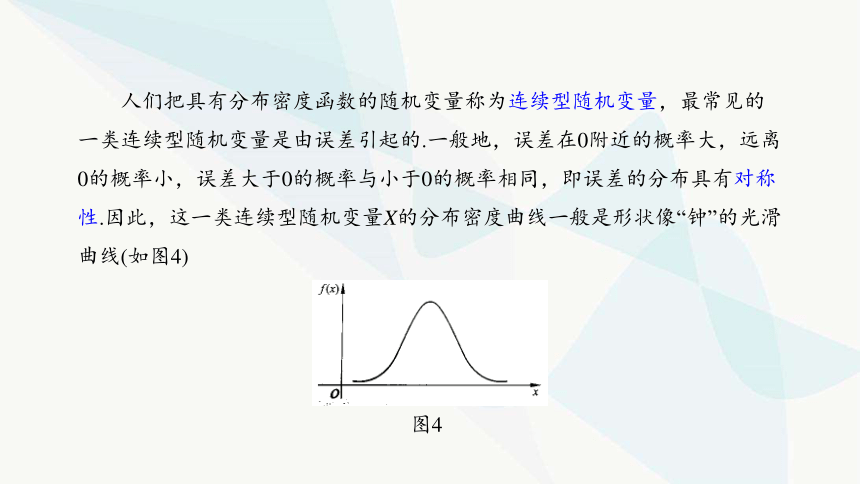
人們把具有分布密度函數(shù)的隨機變量稱為連續(xù)型隨機變量，最常見的一類連續(xù)型隨機變量是由誤差引起的.一般地，誤差在0附近的概率大，遠(yuǎn)離0的概率小，誤差大于0的概率與小于0的概率相同，即誤差的分布具有對稱性.因此，這一類連續(xù)型隨機變量X的分布密度曲線一般是形狀像“鐘”的光滑曲線(如圖4)
圖4
概念生成
由誤差引起的連續(xù)型隨機變量其分布密度函數(shù)圖象如圖4，對應(yīng)的分布密度函數(shù)解析式為
其中實數(shù)μ，σ(σ>0)為參數(shù)，這一類隨機變量X的分布密度(函數(shù))稱為正態(tài)分布密度(函數(shù))，簡稱正態(tài)分布，對應(yīng)的圖象為正態(tài)分布密度曲線，簡稱為正態(tài)曲線.
正態(tài)分布是最常見、最重要的連續(xù)型隨機變量的分布，是刻畫誤差分布的重要模型，因此也稱為誤差模型.
如果隨機變量X服從正態(tài)分布，那么這個正態(tài)分布完全由參數(shù)μ，σ(σ>0)確定，記為X~N(μ，σ2).其中EX=μ,DX=σ2.曲線與x軸之間的面積為1.
正態(tài)分布的特點：
如果一個隨機變量X服從正態(tài)分布，那么對于任何實數(shù)a,b(a正態(tài)曲線有如下性質(zhì)：
(1)曲線在x軸的上方，與x軸不相交.
(2)曲線是單峰的，關(guān)于直線x=μ對稱.
(3)曲線的最高點位于x=μ處.
(4)當(dāng)x<μ時，曲線上升；當(dāng)x>μ時，曲線下降；并且當(dāng)曲線向左、右兩邊無限延伸時，以x軸為漸近線(如圖).
思考：一個正態(tài)分布完全由參數(shù)μ和σ確定，這兩個參數(shù)對正態(tài)曲線的形狀有何影響 它們反映正態(tài)分布的哪些特征
(1)當(dāng)參數(shù)σ取定值時：
μ3= -1
μ1=0　
μ2=1
x
y
若σ固定， 圖像位置隨μ值的變化而沿x軸平移
σ=1
為位置參數(shù)

2 =0.5
1 =1
3=2
μ=0　
x
y
(2)當(dāng)參數(shù)μ取定值時：
若μ固定，σ越大， 曲線越“矮胖”，表示總體的分布越分散；
σ越小， 曲線越“高瘦”，表示總體的分布越集中.
為形狀參數(shù)

一次教學(xué)質(zhì)量檢測中，甲、乙、丙三科考試成績的正態(tài)分布密度曲線如圖所示，下列說法中正確的是（ ）
A.甲科總體的標(biāo)準(zhǔn)差最小
B.丙科總體的平均數(shù)最小
C.乙科總體的標(biāo)準(zhǔn)差及平均數(shù)都比甲小，比丙大
D.甲、乙、丙總體的平均數(shù)不相同
練一練
A

(μ-σ，μ+σ]：68.3%,(μ-2σ，μ+2σ]：95.4%,(μ-3σ，μ+3σ]：99.7%.
在區(qū)間(μ-3σ，μ+3σ]外取值的概率為：1-99.7%=0.3%.
特別地，
通常認(rèn)為這種情況在一次試驗中幾乎是不可能發(fā)生的，認(rèn)為是小概率事件.因此，在實際應(yīng)用中，通常認(rèn)為服從正態(tài)分布N(μ,σ)的隨機變量X只取區(qū)間
(μ-3σ，μ+3σ]之間的值，并稱之為3σ原則.
例1 根據(jù)正態(tài)曲線的函數(shù)解析式，找出其均值μ和標(biāo)準(zhǔn)差σ.
(1) ; (2)
(1)μ=0,σ=1;
解:將所給的函數(shù)解析式與正態(tài)分布密度函數(shù)的解析式
對照可得.
(2)μ=1,σ= .
例2 某設(shè)備在正常運行時，產(chǎn)品的質(zhì)量服從正態(tài)分布，其參數(shù)分別為μ=500g,
σ=1g.為了檢查設(shè)備運行是否正常，質(zhì)量檢查員需要隨機地抽取產(chǎn)品，測量其質(zhì)量.當(dāng)檢查員隨機地抽取一個產(chǎn)品，測得其質(zhì)量為504g時，他立即要求停止生產(chǎn)，檢查設(shè)備，他的決定是否有道理？
解:∵產(chǎn)品的質(zhì)量服從正態(tài)分布，μ=500g,σ=1g,
∴根據(jù)正態(tài)分布的性質(zhì)可知產(chǎn)品質(zhì)量在區(qū)間（μ-3σ，μ+3σ],
即（497,503]之間的概率約為99.7%，而產(chǎn)品的質(zhì)量超出這個范圍的概率只有0.3%，這是一個幾乎不可能發(fā)生的事件.
而504g不在這個范圍內(nèi),這說明設(shè)備的運行可能不正常，
因此檢查員的決定是有道理的.
某廠生產(chǎn)的圓柱形零件的外直徑X(單位：cm)服從正態(tài)分布N(4,0.52).質(zhì)檢人員從該廠生產(chǎn)的1 000件零件中隨機抽查1件，測得它的外直徑為5.7 cm，試問：該廠生產(chǎn)的這批零件是否合格？
解:由于外直徑X~N(4,0.52)，
則X在[4-3×0.5,4+3×0.5]之內(nèi)取值的概率為99.7%，在[2.5,5.5]之外取值的概率為0.3%，
而5.7 [2.5,5.5]，這說明在一次試驗中，出現(xiàn)了幾乎不可能發(fā)生的小概率事件，據(jù)此可以認(rèn)為這批零件是不合格的.
練一練
針對本節(jié)課所學(xué)內(nèi)容，說說你都學(xué)到了哪些知識？
正態(tài)分布
應(yīng)用
概率的計算
密度曲線的特征
3σ原則
正態(tài)密度函數(shù)
分布參數(shù)的意義
正態(tài)密度曲線

展開更多......

收起↑