資源簡介

(共26張PPT)
1.1.2 有理數
第1章 有理數
【華東師大版·2024】數學 七年級上冊
授課教師：********
班 級：********
時 間：********
幻燈片 1：封面
標題：1.1.2 有理數的分類標準，能正確對有理數進行分類。
理解有理數的概念，明確有理數的范圍，體會分類思想在數學中的應用。
幻燈片 3：復習引入
回顧：上節課學習了正數和負數，知道像 3、1.5、\(\frac{1}{2}\)這樣的數是正數，像 - 3、-1.5、-\(\frac{1}{2}\)這樣的數是負數，0 既不是正數也不是負數。
提問：我們學過的數有正數、負數和 0，這些數可以統稱為哪一類數呢？它們之間又有怎樣的包含關系？
引入：今天我們就來學習一個新的概念 —— 有理數，探究這些數的分類情況。
幻燈片 4：有理數的概念
定義：整數和分數統稱為有理數。
說明：
整數包括正整數、0、負整數，如 1、2、0、-1、-2 等。
分數包括正分數和負分數，如\(\frac{1}{2}\)、3.5、-\(\frac{3}{4}\)、-0.6 等（有限小數和無限循環小數都可以化為分數，因此屬于分數范疇）。
有理數是對整數和分數的統稱，也就是說，有理數要么是整數，要么是分數。
幻燈片 5：有理數的分類（按定義分類）
分類圖：
有理數
├── 整數
│ ├── 正整數（如1、2、3…）
│ ├── 0
│ └── 負整數（如-1、-2、-3…）
└── 分數
├── 正分數（如$\frac{1}{2}$、3.2…）
└── 負分數（如-$\frac{3}{4}$、-0.5…）
示例：將下列數按定義分類：5、-3、0、\(\frac{1}{3}\)、-2.5、7、-\(\frac{4}{7}\)
整數：5、-3、0、7
分數：\(\frac{1}{3}\)、-2.5、-\(\frac{4}{7}\)
幻燈片 6：有理數的分類（按性質符號分類）
分類圖：
有理數
├── 正有理數
│ ├── 正整數（如1、2、3…）
│ └── 正分數（如$\frac{1}{2}$、3.2…）
├── 0
└── 負有理數
├── 負整數（如-1、-2、-3…）
└── 負分數（如-$\frac{3}{4}$、-0.5…）
示例：將下列數按性質符號分類：5、-3、0、\(\frac{1}{3}\)、-2.5、7、-\(\frac{4}{7}\)
正有理數：5、\(\frac{1}{3}\)、7
0：0
負有理數：-3、-2.5、-\(\frac{4}{7}\)
幻燈片 7：有理數分類的注意事項
分類要按同一標準進行，不能交叉分類，如不能既按定義又按性質符號同時分類。
0 是有理數，但它既不是正數也不是負數，在分類時要單獨列出。
整數包括正整數、0、負整數，不要遺漏 0；分數包括正分數和負分數，有限小數和無限循環小數都屬于分數。
無限不循環小數（如 π）不是有理數，因為它們不能化為分數。
幻燈片 8：例題 1—— 判斷是否為有理數
題目：下列各數中，哪些是有理數？
3.14、-5、\(\frac{2}{7}\)、π、0、-0.121221222…（每兩個 1 之間多一個 2）、\(\sqrt{2}\)
解答過程：
3.14 是有限小數，可化為分數，是有理數。
-5 是負整數，是有理數。
\(\frac{2}{7}\)是分數，是有理數。
π 是無限不循環小數，不是有理數。
0 是有理數。
-0.121221222… 是無限不循環小數，不是有理數。
\(\sqrt{2}\)是無限不循環小數，不是有理數。
結論：有理數有 3.14、-5、\(\frac{2}{7}\)、0。
幻燈片 9：例題 2—— 按要求分類
題目：把下列各數分別填入相應的集合里：
-3、\(\frac{1}{5}\)、0、-3.14、7、-\(\frac{2}{3}\)、2.8、-1
正整數集合：{…}
負分數集合：{…}
有理數集合：{…}
解答過程：
正整數是大于 0 的整數，所以正整數集合：{7…}
負分數是小于 0 的分數，所以負分數集合：{-3.14、-\(\frac{2}{3}\)…}
有理數包括整數和分數，所以有理數集合：{-3、\(\frac{1}{5}\)、0、-3.14、7、-\(\frac{2}{3}\)、2.8、-1…}
結論：如上所示。
幻燈片 10：課堂練習 1
題目：下列說法正確的是（ ）
A. 有理數就是整數 B. 有理數包括整數和分數
C. 0 不是有理數 D. 無限小數都是有理數
答案：B
幻燈片 11：課堂練習 2
題目：把下列各數填入相應的括號內：
5、-0.3、0、-7、\(\frac{3}{4}\)、-\(\frac{1}{2}\)、8.6
整數集合：（ ）
正分數集合：（ ）
負有理數集合：（ ）
答案：整數集合：（5、0、-7）；正分數集合：（\(\frac{3}{4}\)、8.6）；負有理數集合：（-0.3、-7、-\(\frac{1}{2}\)）
幻燈片 12：課堂練習 3
題目：判斷對錯：
（1）所有的整數都是有理數。（ ）
（2）所有的分數都是有理數。（ ）
（3）0 是最小的有理數。（ ）
（4）無限循環小數是有理數。（ ）
答案：（1）√；（2）√；（3）×；（4）√
幻燈片 13：易錯點分析
常見錯誤：
認為 0 不是有理數，忽略 0 是整數，屬于有理數范疇。
把無限不循環小數當作有理數，如 π、\(\sqrt{2}\)等，它們不能化為分數，不是有理數。
分類時標準不統一，如將數既歸入整數集合又歸入正數集合，導致分類混亂。
規避方法：
牢記有理數的定義：整數和分數統稱為有理數，0 是整數，因此是有理數。
明確無限不循環小數不是有理數，只有有限小數和無限循環小數才是分數，屬于有理數。
分類時嚴格按照同一標準（要么按定義，要么按性質符號），確保每個數只屬于一個類別（除了整體集合）。
幻燈片 14：課堂小結
有理數的概念：整數和分數統稱為有理數。
分類方法：
按定義：分為整數（正整數、0、負整數）和分數（正分數、負分數）。
按性質符號：分為正有理數（正整數、正分數）、0、負有理數（負整數、負分數）。
注意事項：分類標準要統一，0 是有理數，無限不循環小數不是有理數。
幻燈片 15：布置作業
基礎作業：教材課后練習題第 1、2、3 題（判斷有理數、對有理數進行分類）。
提升作業：自己寫出 5 個有理數，其中包括正整數、負整數、正分數、負分數和 0，并說明它們各自屬于哪一類。
5
課堂檢測
4
新知講解
6
變式訓練
7
中考考法
8
小結梳理
學習目錄
1
復習引入
2
新知講解
3
典例講解
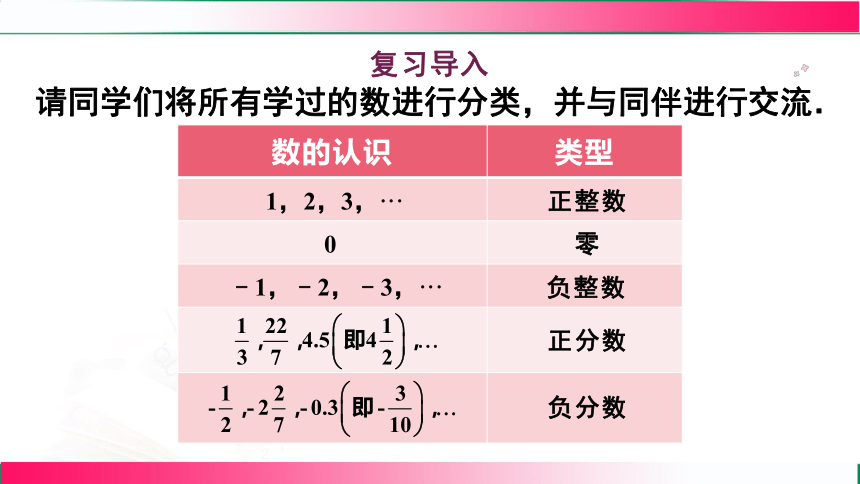
復習導入
請同學們將所有學過的數進行分類，并與同伴進行交流．
數的認識 類型
1，2，3，···
正整數
0
零
﹣1，﹣2，﹣3，···
負整數
正分數
負分數
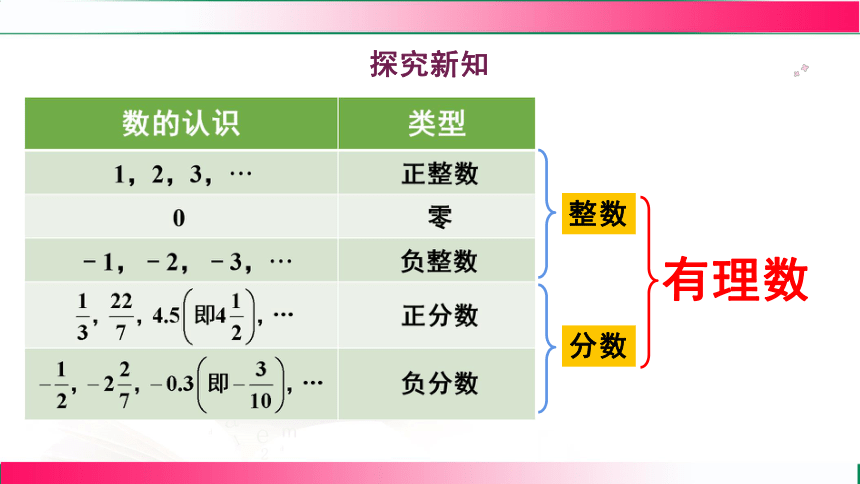
探究新知
整數
分數
有理數
整數和分數統稱為有理數．
有理數的定義
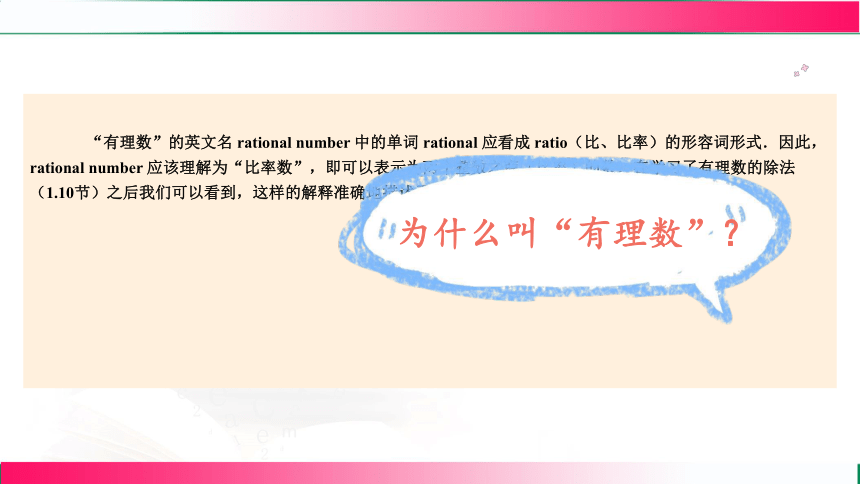
“有理數”的英文名 rational number 中的單詞 rational 應看成 ratio（比、比率）的形容詞形式．因此，rational number 應該理解為“比率數”，即可以表示為兩個整數之商（比率）的數．在學習了有理數的除法（1.10節）之后我們可以看到，這樣的解釋準確地描述了有理數的本質．
為什么叫“有理數”？
有理數
整數
正整數
0
負整數
正分數
負分數
分數
有理數
正有理數
正整數
0
負整數
正分數
負分數
負有理數
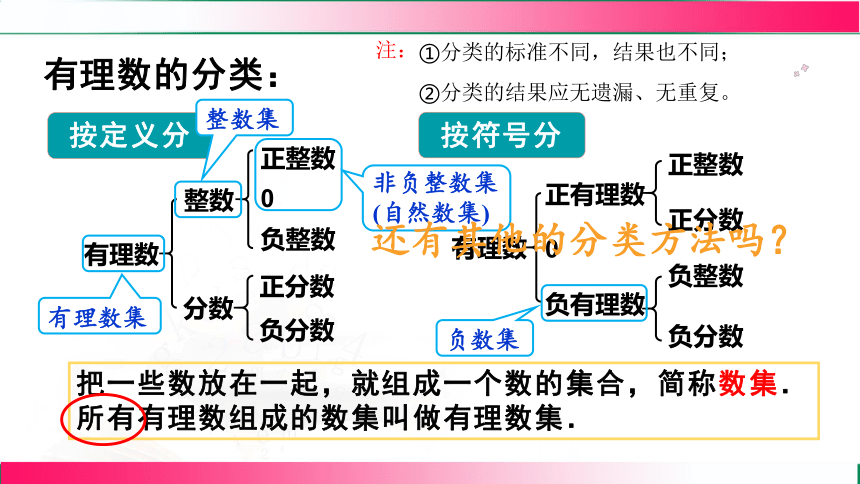
按定義分
按符號分
整數集
有理數集
負數集
非負整數集
(自然數集)
有理數的分類：
還有其他的分類方法嗎？
①分類的標準不同，結果也不同；
②分類的結果應無遺漏、無重復。
注：
把一些數放在一起，就組成一個數的集合，簡稱數集．
所有有理數組成的數集叫做有理數集．
正數集
負數集
整數集
有理數集
例1
把下列各數填入表示它們所在的數集的圈里：
﹣18， 3.1416，0，2023， ﹣0.142857，95%．
都是
3.1416，
2023，
95%
﹣18，
﹣0.142857
﹣18，
0，
2023
正數 負數 整數 分數 有理數
-8
0.9
0
π
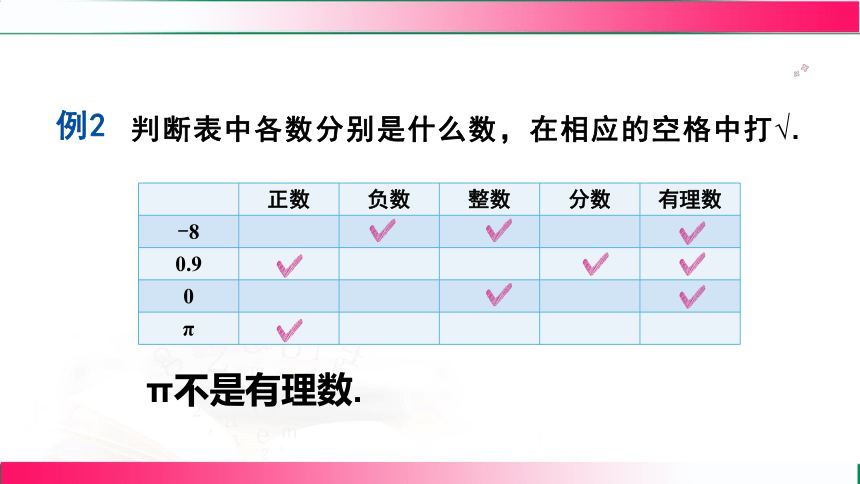
例2
判斷表中各數分別是什么數，在相應的空格中打√.
π不是有理數.
（1）0是整數；（ ） （6）所有的整數都是正數；（ ）
（2）自然數一定是整數；（ ） （7）所有的正數都是整數；（ ）
（3）0是正整數；（ ） （8）一個數不是正數就是負數；（ ）
（4）整數一定是自然數；（ ） （9）分數一定是有理數；（ ）
（5）任何小數都是有理數；（ ） （10）0是最小的有理數.（ ）
例3
判斷下列說法是否正確.
非負整數
無限不循環小數
0
鞏固練習
1．請說出兩個正整數、兩個負整數、兩個正
分數、兩個負分數．它們都是有理數嗎？
【教材P6 練習 第1題】
解：(答案不唯一)兩個正整數：1，2：
兩個負整數：-2，-7；
兩個正分數:
兩個負分數:
它們都是有理數.
2．有理數集中有沒有這樣的數，它既不是正數，
也不是負數？若有，請說出這樣的數．
解：有，它是 0．
【教材P6 練習 第2題】
知識點1 有理數及其相關概念
1.下列各數中，是正整數的是( )
A
A.3 B.2.1 C.0 D.
返回
2.在，0，，， 中，分數有( )
C
A.1個 B.2個 C.3個 D.4個
返回
3.下列說法中，錯誤的是( )
B
A. 是負有理數 B.0不是整數
C.是正有理數 D. 是負分數
返回
知識點2 有理數的分類
4.［2025太原期中］下列說法正確的是( )
D
A.整數就是正整數和負整數
B.0和循環小數不是有理數
C.正有理數和負有理數組成全體有理數
D.整數和分數統稱為有理數
返回
5.［2025鄭州月考］在，，，260，，，0， 中，
正數有___個，負數有___個，正分數有___個，負分數有___個.
4
3
2
2
返回
6.［教材習題 變式］把下列各數填入它所在的數集的大括號里：
，，0，，，，，， .
正整數集：{________…}；
負整數集：{____________…}；
分數集：{_______________________________…}.
，
，，
，，，，，
返回
7.在，，0，，， ，7中，非負數有___個.
4
返回
8.（4分）將各數填入對應數集的圈里：
，，75，，，0，，， .
返回
解：
9.［教材習題 變式］觀察下面的數，直接寫出后面3個數，及第100、
200個數.
（1）1，,0,1，,0,1，,0，___，____，___， ；第100個數是
___，第200個數是____.
（2），，，，，__，____，__， ；第100個數是____，
第200個數是_ ___.
1
0
1
10.（4分） 寫出同時滿足下列條件的五個有理數：
①有1個數既不是正數，也不是負數；②其中3個不是負數；③其中至少
有1個是正分數；④其中只有1個是負整數.
解：1，，0，， .（答案不唯一）
11.（4分）已知，， 三個數集，請把這些數填在下圖中的相應位置.
,，,6, ；
,,,10, }；
2.1，,8, .
解：如圖所示.
返回
有理數按照不同的標準可以分為哪幾類？
課堂小結
有理數
整數
正整數
0
負整數
正分數
負分數
分數
或
有理數
正有理數
正整數
0
負整數
正分數
負分數
負有理數
按定義分
按符號分
整數與分數統稱為有理數．
謝謝觀看！

展開更多......

收起↑