資源簡介

(共28張PPT)
第二章 有理數及其運算
六年級上冊
2 認識有理數
第3課時 絕對值與相反數
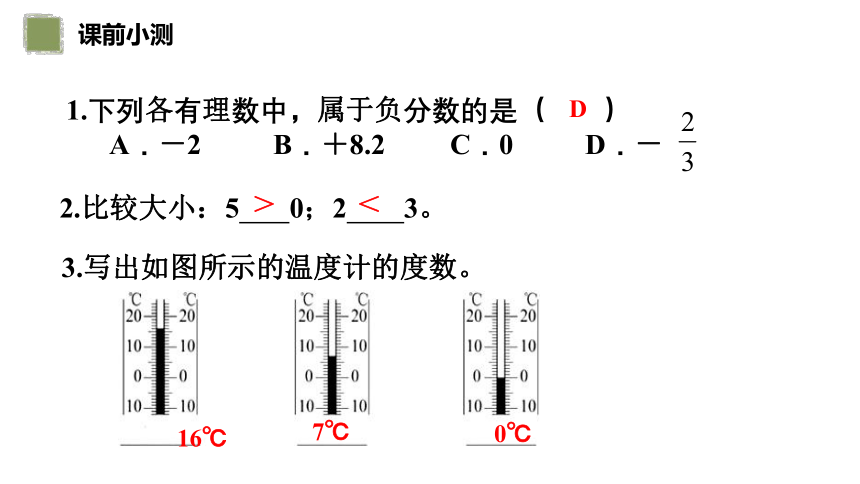
3.寫出如圖所示的溫度計的度數。
課前小測
＞
1.下列各有理數中，屬于負分數的是（　　）
A．－2 B．＋8.2 C．0 D．－
D
2.比較大小：5 0；2 3。
＜
16℃
7℃
0℃
情境導入
壹
目
錄
課堂小結
肆
當堂達標
叁
新知初探
貳
情境導入
壹
情境導入
兩輛汽車從同一處O出發，分別向東、西方向行駛10km，到達A、B兩處。思考：它們行駛的路線相同嗎？它們行駛路程的遠近相同嗎？
新知初探
貳
合作探究
探究活動1　絕對值與相反數的概念
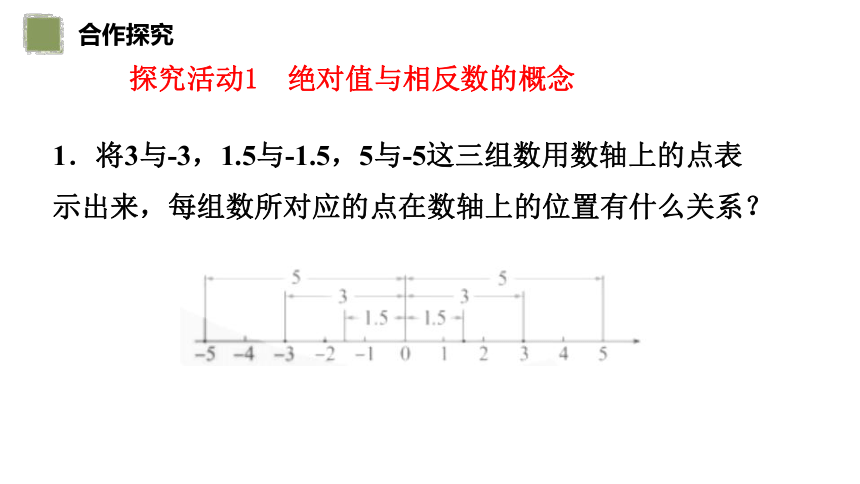
1．將3與-3，1.5與-1.5，5與-5這三組數用數軸上的點表示出來，每組數所對應的點在數軸上的位置有什么關系？
歸納小結
在數軸上,一個數所對應的點與原點之間的距離叫作這個數的絕對值．通常用|a|表示數a的絕對值。
如圖，在數軸上，表示5的點與原點的距離是5，就是說，5的絕對值是5，記作|5|=5；表示-3的點與原點的距離是3，就是說，-3的絕對值是3，記作|-3|=3；表示0的點與原點的距離是0，就是說，0的絕對值是0，記作|0|=0。
合作探究
2．（1）3與-3，1.5與-1.5，5與-5這三組數，有何特點？每組數在數軸上所對應的兩個點的位置關系有何特點？
答案：每組數中的兩個數只有符號不同，它們所對應的兩點分別在原點的兩側，到原點的距離相等。
（2）在數軸上，與原點的距離是2的點有幾個？這些點各表示哪個數？
答案：兩個；分別表示2與－2
歸納小結
（1）符號不同、絕對值相同的兩個數，我們稱其中一個數為另一個數的相反數，也稱這兩個數互為相反數。特別地，0的相反數是0。
（2）在數軸上，表示互為相反數的兩個點，位于原點的兩側，且與原點的距離相等。
合作探究
思考·交流
（1）若a是一個任意數，那么－a一定是負數嗎？
不是，如a=0時，－a=0；
（2）－(－5)表示什么意義？化簡后結果是多少？
－5的相反數，5；
（3）你能借助數軸說明－(－1)=＋1嗎？
在數軸上，－1在原點左側，并離原點1個單位長度，則它的相反數在原點左側，并離原點1個單位長度，這個數是1，即有－(－1)=＋1。
典例分析
例1 根據相反數的意義，化簡下列各數。
歸納小結
（1）在一個數前面加上“－”號，就變為它的相反數，也就是說，數a的相反數是－a．
（2）若a是一個任意數，則當a＞0時，－a＜0；當a=0時，－a=0；當a＜0時，－a＞0．
（3）一般地，有＋(＋a)= a；－(－a)= a；＋(－a)=－a；－(＋a)=－a．
（4）多重符號的化簡方法：“＋”號可以省略不寫，化簡結果的符號取決于正數前“－”號的個數．若有偶數個“－”號，則把“－”號全部去掉；若有奇數個“－”號，則保留一個“－”號，可簡記為“奇負偶正”．
合作探究
探究活動2　絕對值的性質與簡單應用
1．絕對值的性質
填一填，從中發現什么規律
|+2|=　　　　,|+8.2|=　　　　;|0|=　　　　;
|-3|=　　　　,|-0.2|=　　　　,|-8.2|=　　　　.
歸納小結
（1）正數的絕對值是它本身 ; 負數的絕對值
是它的相反數; 0的絕對值是0 .即
①若a>0,則|a|=a;
②若a<0,則|a|=-a;
③若a=0,則|a|=0.
（2）絕對值的非負性
由絕對值的定義可知:不論有理數a取何值,它的絕對值總是正數或0(通常也稱非負數),絕對值具有非負性,即|a|≥0.
典例分析
例2 求下列各數的絕對值:-7,-4.75,10.5.
例3 計算:
(1)|0.32|+|0.3|;　　　　　　(2)|-4.2|-|4.2|.
解：|－7|＝7；|－4|＝4；|75|＝75；|10.5|＝10.5。
解：（1）原式＝0.32＋0.3＝0.62；
（2）原式＝4.2－4.2＝0。
合作探究
思考·交流
2．利用絕對值比較兩個負數的大小
(1)在數軸上表示下列各數,并比較它們的大小:
-1.5,-3,-1,-5.
(2)求出(1)中各數的絕對值,并比較它們的大小.
(3)我發現:兩個負數比較大小，　　　　.
典例分析
例4 比較下列每組數的大小.
(1)-1和-5;
[分析]比較兩個負數大小的步驟:
(1)先求它們的絕對值;
(2)比較它們的絕對值的大小;
(3)根據“兩個負數比較大小,絕對值大的反而小”比較原數的大小.
解:(1)因為|-1|=1,|-5|=5,(首先求出兩個負數的絕對值)1<5,(再比較兩個絕對值的大小)
所以-1>-5.(“根據兩個負數比較大小,絕對值大的反而小”下結論)
典例分析
(2)因為 ,|-2.7|=2.7,(首先求出兩個負數的絕對值)
<2.7,(再比較兩個絕對值的大小)
所以 >-2.7.(根據“兩個負數比較大小,絕對值大的反而小”下結論)
歸納小結
比較兩個負數的大小的步驟：
（1）分別求出兩個負數的絕對值；
（2）比較兩個絕對值的大小；
（3）根據“兩個負數比較大小，絕對值大的反而小”作出正確的判定．
合作探究
3．絕對值的簡單應用
某種食品包裝袋上標注質量為450 g,對6袋該種食品的實際質量進行檢測，檢測結果如下( 用正號表示超過標注質量,用負號表示不足標注質量):
-25，+10，-20，+30，+15， -40。
哪袋食品的實際質量更接近標注質量 為什么
解：|－25|＝25，|＋10|＝10，|－20|＝20，|＋30|＝30，|＋15|＝15，|－40|＝40，因為10＜15＜20＜25＜30＜40，所以第二袋食品的實際質量更接近標準質量．
嘗試·思考
當堂達標
叁
當堂達標
2.﹣1.5相反數的是（　　）
A. B. － C. － D.
A
1. ﹣ 相反數的是（　　）
A. － B. C. －4 D.4
B
當堂達標
3.絕對值最小的有理數是　　　　.
0
4.若 ,則x的相反數是　　　　.
解析:由絕對值的意義可知 ,再由相反數的意義可知 的相反數為 , 的相反數為 .故填 .
5.
＞
課堂小結
肆
課堂小結
通過本節課的學習，你有哪些收獲與困惑？
數形結合思想
分類討論思想
轉化思想
作業布置
詳見教材習題
P43 T1-5
謝
謝

展開更多......

收起↑